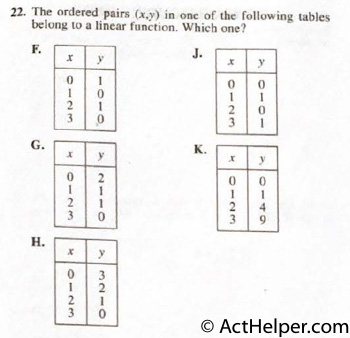
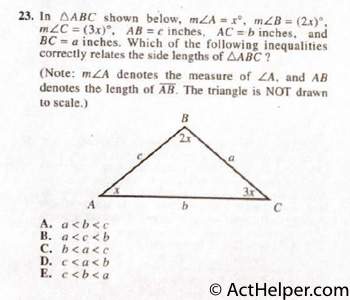
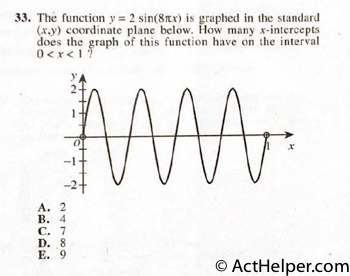
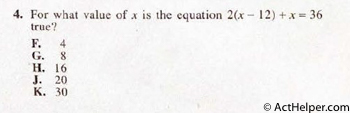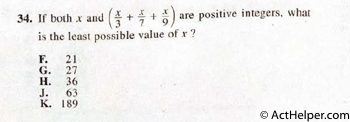Choice B
$$45=1\times3\times3\times5$$ $$50=1\times2\times5\times5$$ $$84=1\times2\times2\times3\times7$$ $$The\ greastest\ common\ factor=1 $$
Choice J
$$\Rightarrow 2x-24+x=36$$ $$\Rightarrow 3x=36+24$$ $$\Rightarrow 3x=60$$ $$\Rightarrow x=20$$
Choice A
$$Total=22$$ $$Not\ white=22-12=10$$ $$P(Not\ white)=\frac{Not\ white}{Total}=\frac{10}{22}=\frac{5}{11}$$
Choice F
$$\frac{1}{2}:12=5:x$$ $$12\times5=\frac{1}{2}x$$ $$60=\frac{1}{2}x$$ $$x=120$$
Choice C
$$\Rightarrow 2x+5=0\ or\ 3x-4=0$$ $$\Rightarrow x=-\frac{5}{2}\ or\ x=\frac{4}{3}$$
Choice C
$$\frac{2}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{60}$$ $$=\frac{40}{60}+\frac{10}{60}+\frac{6}{60}+\frac{1}{60}$$ $$=\frac{40+10+6+1}{60}$$ $$=\frac{57}{60}$$ $$1-\frac{57}{60}=\frac{3}{60}=\frac{1}{20}$$
Choice H
$$7^{2}=49$$ $$8^{2}=64$$ $$\sqrt{61}\lt\sqrt{64}$$ $$\Rightarrow \sqrt{61}\lt8$$
Choice H
$$n=1,\ 1=2n-1,\ 1=3n-2,\ 1=4n-3,\ 1=5n-4,\ 1=6n-5$$ $$n=2,\ 5\neq4-1,\ 5\neq6-2,\ 5=8-3,\ 5\neq10-4,\ 5\neq12-5$$ $$Only\ 4n-3\ is correct.$$
Choice F
$$(\frac{2}{3}+\frac{3}{4})\div2$$ $$=(\frac{8}{12}+\frac{9}{12})\div2$$ $$=\frac{17}{12}\div2$$ $$=\frac{17}{24}$$
Choice C
$$\frac{46+x}{60+x}=0.8$$ $$\Rightarrow 0.8\times(60+x)=46+x$$ $$\Rightarrow 48+0.8x=46+x$$ $$\Rightarrow 0.2x=2$$ $$\Rightarrow x=10$$
Choice A
Let the 9th number be 91 which is greater than 90.
$$The\ mean\ of\ Set\ A=(62+76+76+80+82+87+94+96)\div8=\frac{653}{8}=81.625$$ $$The\ median\ of\ Set\ A=(80+82)\div2=81$$ $$The\ mean\ of\ Set\ B=\frac{653+91}{9}\approx82.66$$ $$The\ median\ of\ Set\ B=82$$ $$\Rightarrow 82.66\gt 81.625$$ $$\Rightarrow 82\gt 81$$The mean and the median of Set B will each be greater than the mean and the median of Set A.
Choice B
$$\Rightarrow \frac{((-5)+3),(8+(-1))}{2}=(-1,\frac{7}{2})$$
Choice H
When the X value is …
Choice A
The larger the angle in …
Choice F
$$y=mx+b$$ $$5=m+b---(1)$$ $$7=17m+b---(2)$$ $$2=16m$$ $$\Rightarrow …
Choice C
$$The\ longer\ side=x+2$$ $$The\ Shorter\ …
Choice F
We assume that x adult …
Choice E
NOT first-time skiers=200-25=175
$$\frac{175}{200}=\frac{x}{8}$$ $$\Rightarrow …Choice H
$$E=\frac{300,000}{t+100}$$ $$t=0 \Rightarrow E=\frac{300,000}{100}=3,000$$
Choice E
Let another side of the …
Choice F
$$C=2A-3B$$ $$\Rightarrow C=2\begin{bmatrix}3 & 5 …
Choice B
Experimental group:
1 min 46 …
Choice K
$$0,1,2,3,4,5,6,7,8,9\rightarrow 10\ numbers$$ $$10\times10\times10=1000$$
Choice C
Choice J
$$3=1\times3$$ $$7=1\times7$$ $$9=1\times3\times3$$ $$\Rightarrow[3,7,9]=1\times3\times3\times7=63$$
Choice D
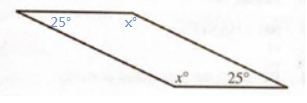
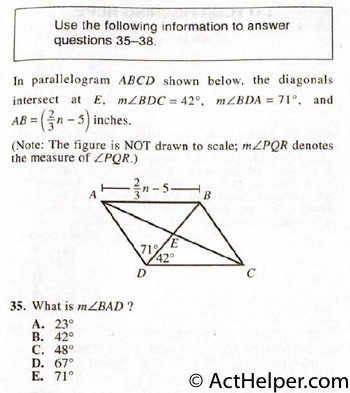
$$\because\ ABCD\ is\ a\ parallelogram.$$ …
Choice K
$$\because\ ABCD\ is\ a\ parallelogram.$$ …
Choice E
$$\frac{2+30}{2}=16$$ $$\frac{10+3}{2}=\frac{13}{2}$$ $$\Rightarrow\ E(16,\frac{13}{2})$$
Choice K
$$\because\ All\ three\ sides\ are\ …
Choice B
$$=(a+\sqrt{b})a-(a+\sqrt{b})(2\sqrt{b})$$ $$=a^{2}+a\sqrt{b}-2a\sqrt{b}-2b$$ $$=a^{2}-a\sqrt{b}-2b$$
Choice H
$$\pi(30)+\pi(50)=80\pi$$ $$\frac{80\pi}{75}=\frac{80(3.14)}{75}=3.3493$$
Choice B
$$(\frac{4}{5})^{-\frac{3}{2}}=(\frac{5}{4})^{\frac{3}{2}}=\frac{5^{\frac{3}{2}}}{4^{\frac{3}{2}}}$$ $$=\frac{5^{1}\times5^{\frac{1}{2}}}{(2^{2})^{\frac{3}{2}}}$$ $$=\frac{5^{1}\times5^{\frac{1}{2}}}{8}=\frac{5\sqrt{5}}{8}$$
Choice F
$$\frac{1}{25}=5^{-2}$$ $$\log_{x}{5^{-2}}=-2$$ $$\Rightarrow x^{2}=5^{-2}$$ $$\Rightarrow …
Choice D
$$y=mx+b$$ $$(-4,-5)\rightarrow -5=-4m+b$$ $$(0,-3)\rightarrow -3=0m+b …
Choice G
$$16=4\times4$$ $$28=4\times7$$ $$[16,28]=4\times4\times7=112$$
Choice D
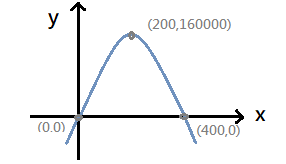
$$p(c)=1600c-4c^{2}=-4c^{2}+1600c$$ $$=-4c(c-400)$$ $$\Rightarrow c=0,\ c=400$$ …
Choice H
$$a\lt b\lt c\lt d,$$ $$Let\ …
Choice A
$$The\ ratio\ of\ the\ area\ …
Choice G
$$\sqrt{5}\approx2.23$$ $$-1\leq x-\sqrt{5}\leq 4$$ $$\Rightarrow …
Choice D
$$The\ maximum\ force=kSv^{2}$$ $$50=k(1)(40)^{2}=1600k$$ $$\Rightarrow …
Choice J
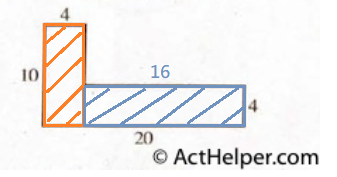
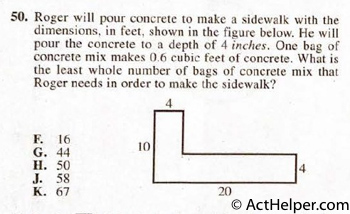
$$4(10)+16(4)=40+64=104$$ $$104\times4=416$$ $$\frac{416}{12}=34.6$$ $$34.6\div0.6=57.7$$
Choice E
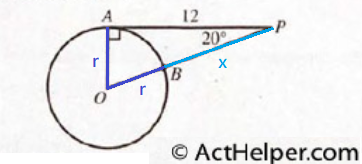
$$\sin 20°=\frac{\overline{OA}}{\overline{OP}}=\frac{r}{r+x}=0.342$$ $$\Rightarrow(r+x)0.342=r$$ $$\Rightarrow(4.368+x)=\frac{4.368}{0.342}=12.77$$ $$\Rightarrow …
Choice J
The average of 10 test …
Choice E
$$27^{n^{2}}=9^{5n-4}$$ $$\Rightarrow (3^{3})^{n^{2}}=(3^{2})^{5n-4}$$ $$\Rightarrow 3^{3(n^{2})}=3^{2(5n-4)}$$ …
Choice G
$$Less\ than\ 6: $$ $$(1,1),(1,2),(1,3),(1,4),$$ …
Choice D
$$68\times x=240-57\times x$$ $$68x=240-57x$$ $$125x=240$$ …
Choice J
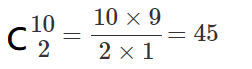
Choice A
$$\frac{(n+1)!6!}{n!3!}$$ $$=\frac{(n+1)!(6\cdot5\cdot4\cdot3\cdot2\cdot1)}{n!(3\cdot2\cdot1)}$$ $$=\frac{(n+1)!(6\cdot5\cdot4)}{n!}$$ $$=\frac{n!(n+1)(6\cdot5\cdot4)}{n!}$$ $$=(n+1)(6\cdot5\cdot4)$$ …
Choice G
I.
1,2,3,4
24,25,26,27
24, 25, …
Choice E
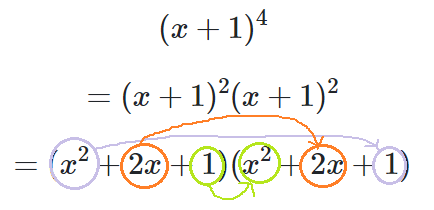
$$(x+1)^{4}$$ $$=(x+1)^{2}(x+1)^{2}$$ $$=(x^{2}+2x+1)(x^{2}+2x+1)$$ $$x^{2}(1)+2x(2x)+1(x^{2})$$ $$=2x^{2}+4x^{2}$$ …
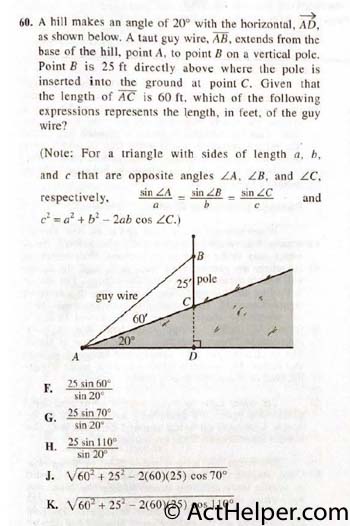
Choice K
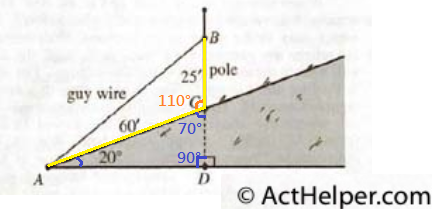
$$c^{2}=60^{2}+25^{2}-2(60)(25)\cos 110°$$ $$c=\sqrt{60^{2}+25^{2}-2(60)(25)\cos 110°}$$