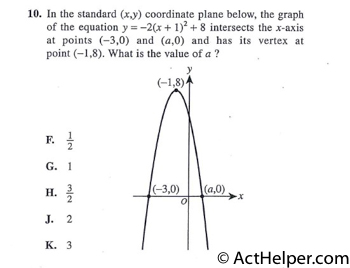
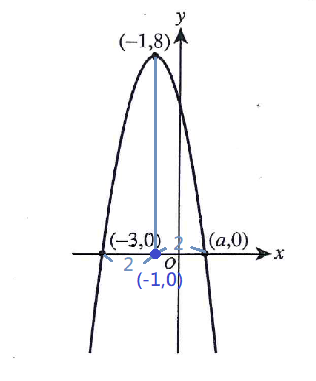
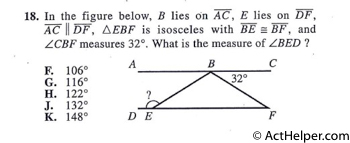
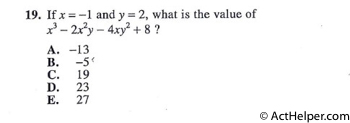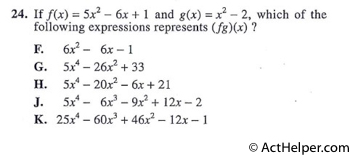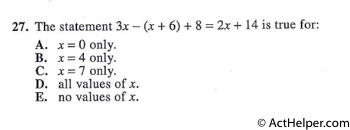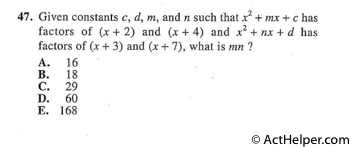Choice C
$$\frac{1}{3}\pi r^{2}h,\ r=3,\ h=6$$ $$\Rightarrow \frac{1}{3}\pi\times3^{2}\times6=18\pi$$
Choice F
$$=\begin{bmatrix}5+(-6) & 7+3 \\(-4)+6 & 4+8 \end{bmatrix}$$ $$=\begin{bmatrix}-1 & 10 \\2 & 12 \end{bmatrix}$$
Choice A
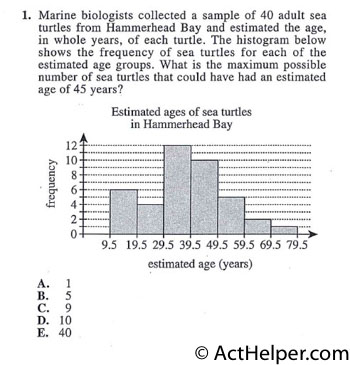
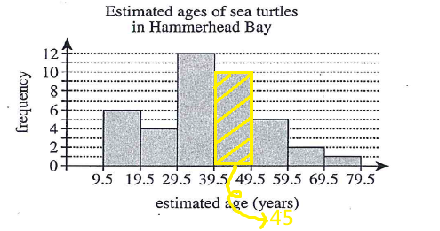
$$60\times\frac{1}{2}=30$$ $$60\times\frac{1}{4}=15$$ $$60\times\frac{1}{6}=10$$ $$60-30-15-10=5$$
Choice J
$$6x-2\leq11.2$$ $$\Rightarrow 6x\leq13.2$$ $$\Rightarrow x\leq2.2$$
2 is the greatest solution.
Choice D
$$17.5+0.7x\leq50$$ $$\Rightarrow 0.7x\leq 32.5$$ $$\Rightarrow x\leq46.42...$$ $$Ans:\ x=46$$
Choice K
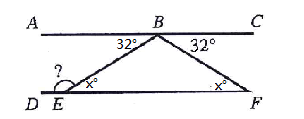
$$\because\overline{BE}\equiv\overline{BF}$$ $$\therefore ABE=\angle CBF=32°$$ $$\because\overline{AC}\parallel\overline{DF}$$ $$\therefore\angle ABE=\angle BEF=32°$$ $$\angle BED=180°-32°=148°$$
Choice C
$$x=-1, y=2, $$ $$x^{3}-2x^{2}y-4xy^{2}+8$$ $$=(-1)^{3}-2(-1)^{2}\times2-4(-1)\times2^{2}+8$$ $$=-1-2\times2+4\times4+8$$ $$=-1-4+16+8$$ $$=19$$
Choice H
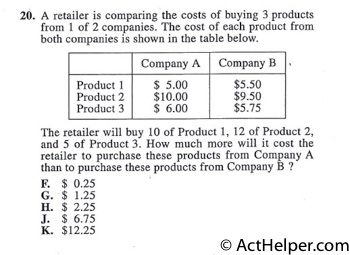
$$A: 10\times5+12\times10+5\times6=200$$ $$B: 10\times5.5+12\times9.5+5\times5.75$$ $$=55+114+28.75$$ $$=197.75$$ $$200-197.75=2.25$$
Choice E
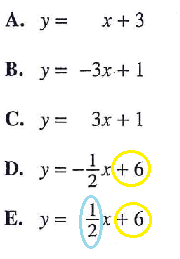
$$Slope\ l=1$$ $$\Rightarrow Slope\ p=1\times\frac{1}{2}=\frac{1}{2}$$ …
Choice H
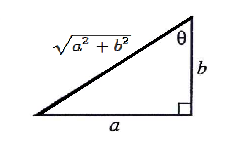
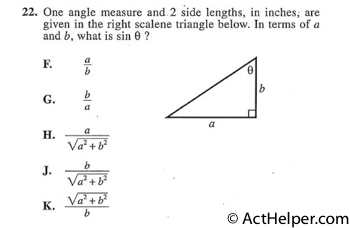
$$\sin\theta=\frac{a}{\sqrt{a^{2}+b^{2}}}$$
Choice E
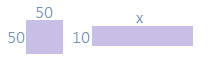
$$50\times50=2500$$ $$10\times x=2500$$ $$\Rightarrow x=250$$
Choice J
$$(fg)(x)=(5x^{2}-6x+1)(x^{2}-2)$$ $$=(5x^{2}-6x+1)(x^{2})-(5x^{2}-6x+1)2$$ $$=(5x^{4}-6x^{3}+x^{2})-10x^{2}+12x-2$$ $$=5x^{4}-6x^{3}-9x^{2}+12x-2$$
Choice B
$$Total\ marbles:\ 12+14+8=34$$ $$p(red)=\frac{12+x}{34+x}=\frac{3}{5}$$ $$5(12+x)=3(34+x)$$ …
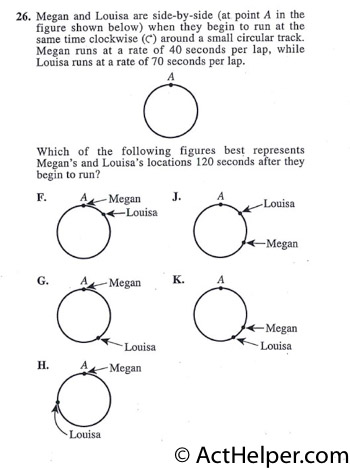
Choice H
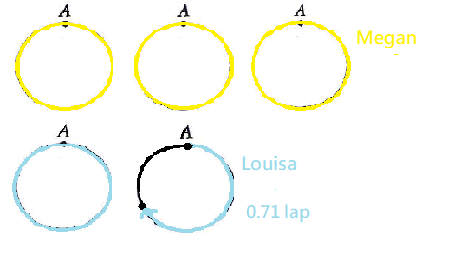
$$Megan:\frac{120}{40}=3$$ $$Louisa:\frac{120}{70}=1\frac{5}{7}\approx1.71$$
Choice E
$$\require{cancel} $$ $$3x-(x+6)+8=2x+14$$ $$\Rightarrow3x-x-6+8=2x+14$$ $$\Rightarrow\cancel{2x}+2=\cancel{2x}+14$$ …
Choice F
$$Mean:(\frac{1+2+3+4+5+6+7}{2})\div7$$ $$=\frac{[(1+7)7]\div2}{2}\div7$$ $$=\frac{56\div2}{2}\div7$$ $$=\frac{28}{2}\div7$$ $$=14\div7$$ …
Choice C
$$(-2i+5)(2i+5)=(-2i)2i+(-2i)5+5(2i)+5(5)$$ $$=-4i^{2}-10i+10i+25=25-4i^{2}$$ $$Since\ i^{2}=-1,$$ $$\Rightarrow …
Choice H
$$3.8\times10^{5}+6.4\times10^{4}$$ $$=3.8\times10^{1}\times10^{4}+6.4\times10^{4}$$ $$=38\times10^{4}+6.4\times10^{4}$$ $$=(38+6.4)\times10^{4}$$ $$=44.4\times10^{4}$$ …
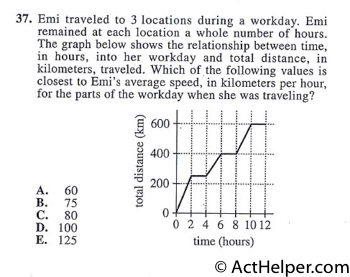
Choice B
Choice F

$$350\ miles\ of\ highway\ driving.$$ …
Choice B
$$$2400\div$4/gallon=600$$ $$600\times25=15000$$
Choice H
$$2400\times5=12000$$ $$12000+3500=15500$$ $$15500\div5=3100$$
Choice C
$$240\ miles=240\times5280\ feet$$ $$1\ hour=3600\ …
Choice H
$$\frac{$2.4}{16}=$0.15\ /ounces$$ $$$0.15\times10=$1.5$$
Choice D
Choice G
The denominator of any fraction …
Choice E
$$0.1\times3+0.7\times4+0.2\times5$$ $$=0.3+2.8+1=4.1$$
Choice K
Cannot be determined from the …
Choice B
$$\mid a-b-1 \mid \gt0$$ $$\Rightarrow …
Choice G
$$2\pi r=2\times3.14\times5=31.4$$ $$150-31.4=118.6$$ $$118.6\div4=29.65$$
Choice D
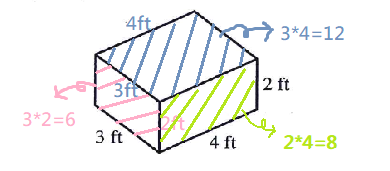
$$3\times4=12$$ $$3\times2=6$$ $$2\times4=8$$ $$(12+6+8)\times2=52$$ $$52\times$0.01=$0.52$$
Choice F
$$Cans:0.05+0.03=$0.08$$ $$Bottles:0.1+0.02=$0.12$$ $$200($0.15-$0.08)+300($0.18-$0.12)$$ $$=200($0.07)+300($0.06)$$ $$=$14+$18=$32 …
Choice B
$$\frac{0.1}{0.18}\approx. 0.56$$
Choice F
The recycling center sold x …
Choice D
$$x^{2}+mx+c=(x+2)(x+4)$$ $$=x^{2}+2x+4x+8$$ $$=x^{2}+6x+8$$ $$\Rightarrow m=6,\ …
Choice G
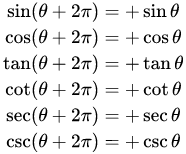
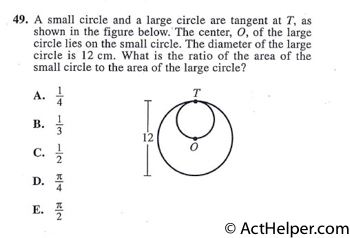
Choice A
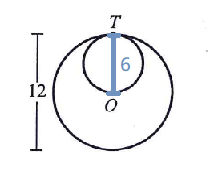
$$Small\ circle\ :\ Large\ circle$$ …
Choice J
$$\frac{2a}{b}+\frac{b}{2a}$$ $$=\frac{2a\times2a}{b\times2a}+\frac{b\times b}{2a\times b}$$ $$=\frac{4a^{2}+b^{2}}{2ab}$$
Choice B
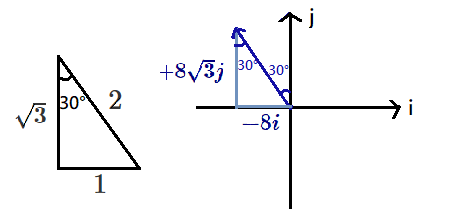
Choice G
$$f(g(x))=\sqrt[3]{x+1}-2$$ $$g(x)=x+1$$ $$f(x)=\sqrt[3]{x}-2$$ $$g(f(x))=(\sqrt[3]{x}-2)+1=\sqrt[3]{x}-1$$
Choice A
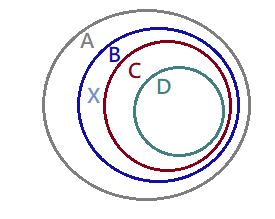
Choice J
$$x^{\frac{4}{6}}\cdot x^{\frac{4}{3}}$$ $$=x^{\frac{4}{6}}\cdot x^{\frac{8}{6}}$$ $$=x^{\frac{4}{6}+\frac{8}{6}}$$ …
Choice A
$$\frac{3}{2}:\frac{2.5}{1.5}$$ $$=\frac{3}{2}:\frac{25}{15}$$ $$=\frac{3}{2}:\frac{5}{3}$$ $$=\frac{3}{2}\times\frac{3}{5}$$ $$=\frac{9}{10}$$
Choice J
$$P(Blue\ Cards)+P(17)-P(Blue\ 17)$$ $$=\frac{20}{100}+\frac{1}{20}-\frac{1}{100}$$ $$=\frac{20}{100}+\frac{5}{100}-\frac{1}{100}$$ …
Choice C
$$City's population:\ x$$ $$x\times1.2\times1.3\times0.8=1.248x$$ $$1.248x-x=0.248x$$
Choice K

$$\Rightarrow\frac{1}{3}$$
Choice A
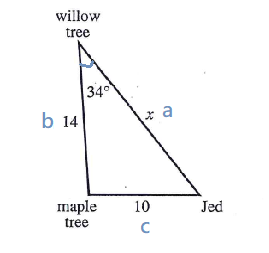
$$c^{2}=a^{2}+b^{2}-2ab\cos\angle C$$ $$\Rightarrow 10^{2}=x^{2}+14^{2}-2ab\cos\angle 34°$$
Choice F