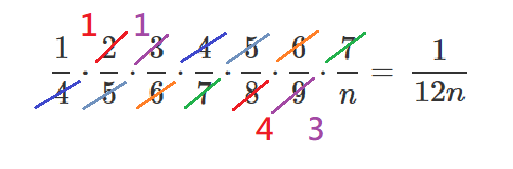
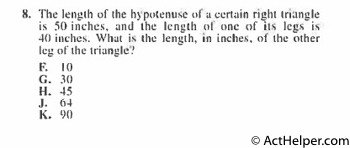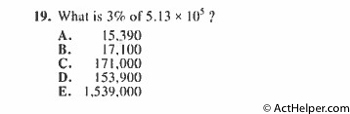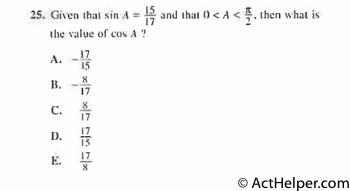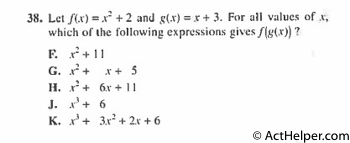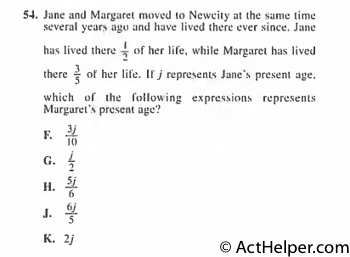Choice E
$$3x-7=5x-13$$ $$\Rightarrow(3x−7)-3x+13=(5x-13)-3x+13$$ $$\Rightarrow6=2x$$ $$\Rightarrow x=3$$
Choice H
$$1\sim40\ hours:$14/hour $$ $$Over\ 40\ hours:$14\times 1\frac{1}{2}=$21/hour $$ $$\Rightarrow$14\times40+$21\times8=$560+$168=$728 $$
Choice B
The rate of leaking water is 4 gallons per minute.
$$\because The\ rate\ of\ leaking\ water\ is\ 4\ gallons\ per\ minute.$$ $$After\ t\ minutes \Rightarrow 4 \times t$$ $$ \Rightarrow G(t)=200-4t$$Choice F
$$(x^{5}y^{3}z^{2})(x^{4}y^{3}z^{6})$$ $$=x^{(5+4)}y^{(3+3)}z^{(2+6)}$$ $$=x^{9}y^{6}z^{8}$$
Choice D
$$-12,24,-48,96,-192,...$$ $$-12\times-2=24$$ $$24\times-2=-48$$ $$-48\times-2=96$$ $$96\times-2=-192$$ $$-192\times-2=384$$
Choice K
$$\require{cancel} $$ $$50 \times\frac{miles}{hour} = 50 \times\frac{miles}{60 minutes}=\frac{5}{6}\times\frac{miles}{minute}$$ $$\Rightarrow120\ miles\div(\frac{5}{6}\times\frac{miles}{minute})=120\ \cancel{miles}\times(\frac{6}{5}\times\frac{minute}{\cancel{miles}})=144\ minutes$$
Choice B
$$6-\frac{1}{2}-1\frac{3}{4}=\frac{24}{4}-\frac{2}{4}-\frac{7}{4}$$ $$=\frac{24-2-7}{4}=\frac{15}{4}=3\frac{3}{4}$$
Choice G
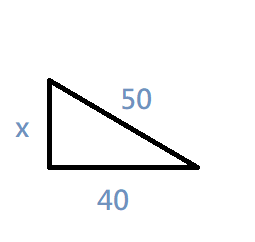
$$x^{2}+40^{2}=50^{2}$$ $$\Rightarrow x^{2}=2500-1600=900$$ $$\Rightarrow x=30$$
Choice D
8% of the spaces are reserved for handicapped parking. That means 92% NOT served for handicapped parking.
$$450\times \frac{92}{100}=414$$Of those parkinf spaces NOT reserved for handicapped parking, 18 are suitable for compact cars only.
$$\Rightarrow 414-18=396 $$Choice J
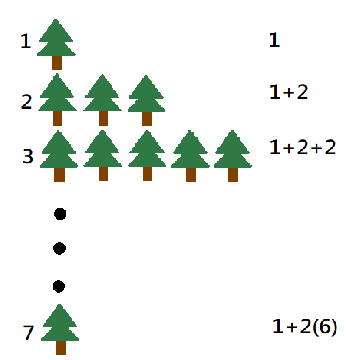
raw1=1,raw2=1+2,raw3=1+2(2),raw4=1+2(3),...,raw7=1+2(6)=13
$$\Rightarrow (1+13)7\frac{1}{2}=49$$Choice C
$$\frac{a}{b^{2}}+\frac{c}{2}$$ $$=\frac{3}{5^{2}}+\frac{8}{2}$$ $$=\frac{3}{25}+4=\frac{103}{25}$$
Choice G
$$21\Rightarrow3\times7$$ $$12\Rightarrow3\times4=3\times2\times2=3\times2^{2}$$ $$8\Rightarrow2\times2\times2=2^{3}$$ $$\Rightarrow 2^{3}\times 3\times7=168$$
Choice C
$$1440=180\times(n-2)$$ $$\Rightarrow\frac{1440}{180}=n-2$$ $$\Rightarrow 8=n-2$$ $$\Rightarrow n=10$$
Choice F
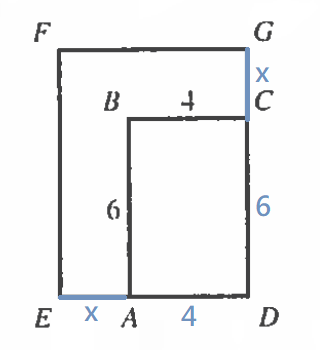
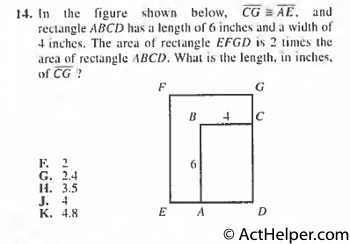
$$Let\ \overline{CG}\equiv\overline{AE}=x$$ $$24\times2=(x+6)(x+4) $$ $$\Rightarrow 48=x^{2}+10x+24 $$ $$\Rightarrow x(x+10)=24 $$ $$\Rightarrow x=2 $$
Choice H
$$x^{2}+3x-54=0$$ $$\Rightarrow (x+9)(x-6)=0$$ $$\Rightarrow x=-9,6$$ $$\Rightarrow -9+6=-3$$
Choice A
$$\require{cancel} $$ $$5.13\times10^{5}\times\frac{3}{100}$$ $$=5.13\times1000\cancel{00}\times\frac{3}{\cancel{100}}$$ $$=5.13\times1000\times3$$ $$=15390$$
Choice K
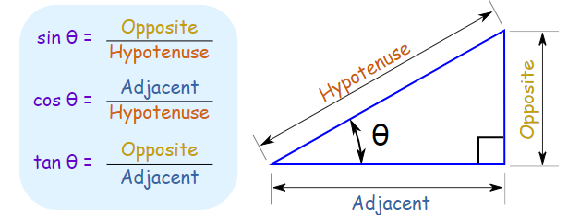
$$\tan\theta=\frac{x}{10}$$ $$\Rightarrow x=\frac{\tan35°}{10}=\frac{1}{10}\tan35°$$
Choice B
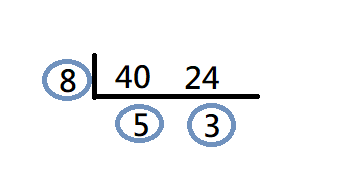
$$\left[40,24\right]=8\times5\times3=120$$ $$120\div40=3$$
3,12,15,24 are multiples …
Choice K
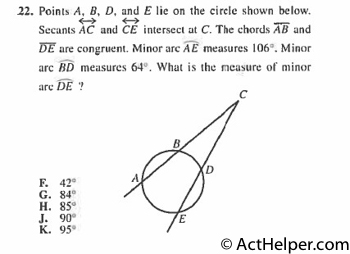
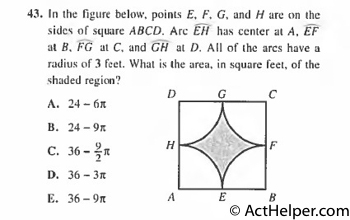
$$\overline{AB}=\overline{DE}\Rightarrow\widehat{AB}=\widehat{DB}=x$$ $$\widehat{AB}+\widehat{DB}+\widehat{AE}+\widehat{BD}=360°$$ $$\Rightarrow 2x+64°+106°=360°\Rightarrow 2x=190° …
Choice B
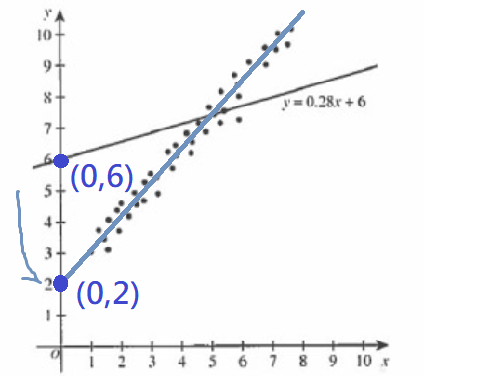
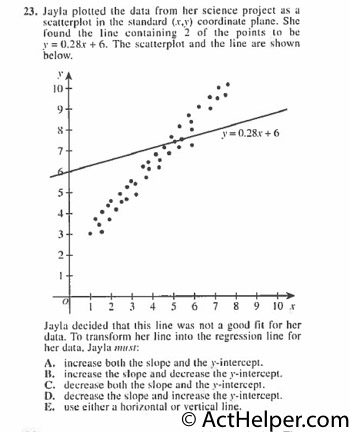
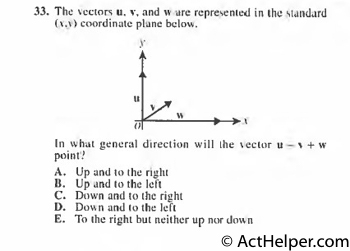
The slope needs to be …
Choice K
$$P(A)+P(B)$$ $$=0.2+0.6$$ $$=0.8$$
Choice C
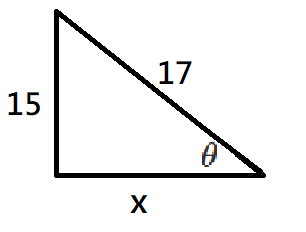
$$\sin A=\frac{15}{17} $$ $$17^{2}=15^{2}+x^{2}$$ $$\Rightarrow …
Choice J
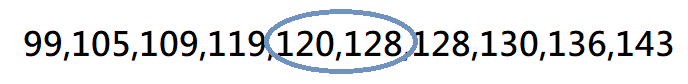
$$(120+128)\div2=124$$
Choice A
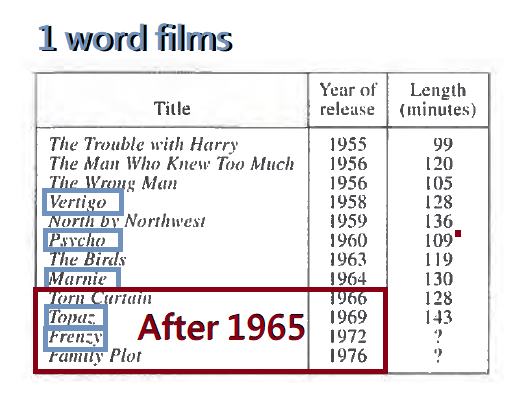
$$\frac{1\ word\ films}{After\ 1965}=\frac{2}{4}$$
Choice G
The new version is 20% …
Choice A
Tapaz=143 minutes
Frenzy= x minutes …
Choice K
$$A-B =\begin{bmatrix}3 & -5 \\-2 …
Choice A
Cent is a unit of …
Choice H
$$(3x-y)7=(x+y)4$$ $$\Rightarrow 21x-7y=4x+4y$$ $$\Rightarrow 17x=11y$$ …
Choice A
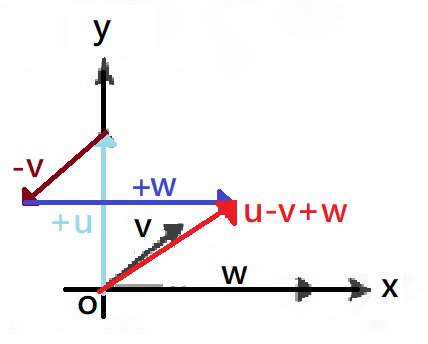
Choice H
$$11\ feet\ 4\ inches =11\times12+4=132+4=136\ …
Choice D
$$(kx+m)(rx+n)$$ $$=krx^{2}+knx+mrx+mn$$ $$=krx^{2}+(kn+mr)x+mn$$
Choice J
$$(F)\frac{15}{101}\lt\frac{15}{100}$$ $$(G)\frac{150}{999}\lt\frac{150}{1000}(=\frac{15}{100})$$ $$(H)0.15=\frac{15}{100}$$ $$(J)0.\overline{15}=0.151515...\gt\frac{15}{100}$$ $$(K)0.\overline{151}=0.151151...(\lt0.151515...)$$ …
Choice D
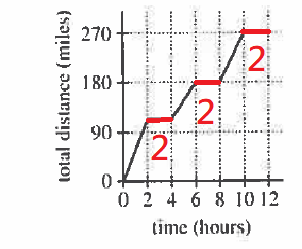
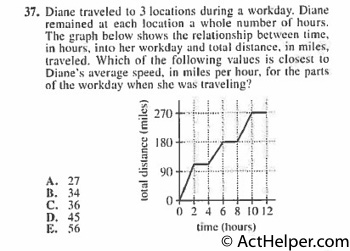
$$2+2+2=6$$ $$12-6=6$$ $$270\div6=45$$
Choice H
$$f(x)=x^{2}+2, g(x)=x+3$$ $$f(g(x))=f(x+3)$$ $$=(x+3)^{2}+2$$ $$=(x+3)(x+3)+2$$ …
Choice C
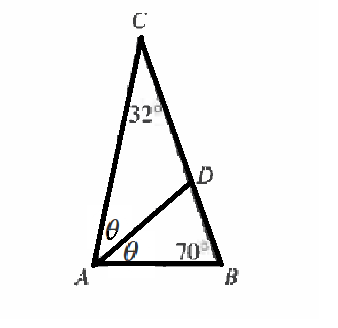
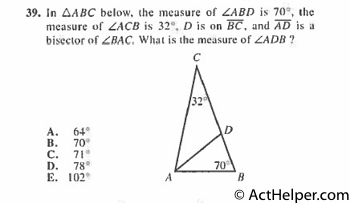
$$\overline{AD}\ is\ a\ bisector\ of\ …
Choice F
$$\because x=4\ ,\ 4\geq4$$ $$f(4)=-\frac{1}{2}x-3=-\frac{1}{2}\times4-3=-2-3=-5$$
Choice D
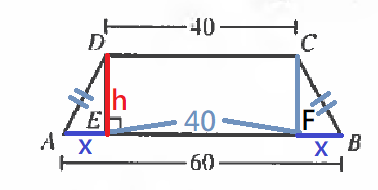
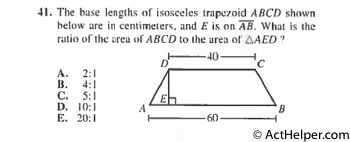
$$\because ABCD\ is\ isosceles\ trapezoid$$ …
Choice F
$$5^{2x}=25^{2}$$ $$5^{2x}=(5^{2})^{2}$$ $$5^{2x}=5^{4}$$ $$\Rightarrow 2x=4$$ …
Choice E
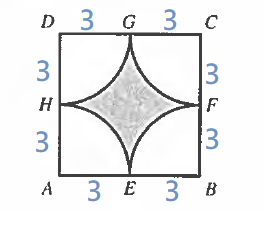
$$Area\ of\ circle=\pi \times r^{2} …
Choice J
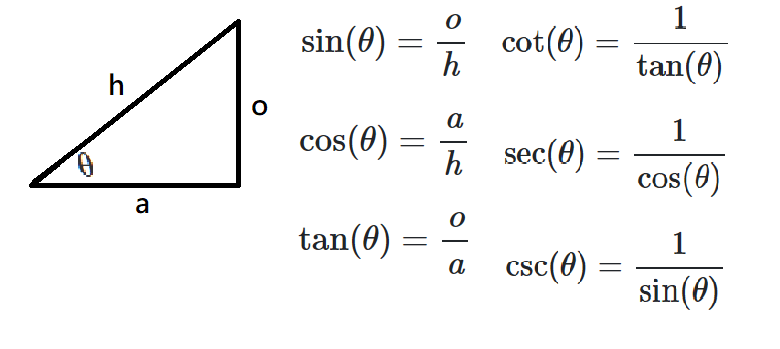
$$\tan x=\frac{o}{a},\ \sin x=\frac{o}{h},\ \cos …
Choice D
The original price is x. …
Choice G
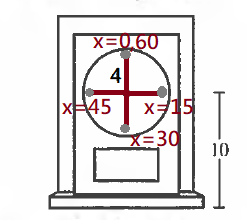
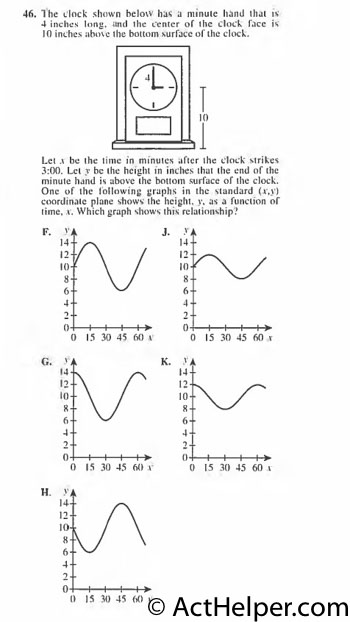
Let x be the time …
Choice D
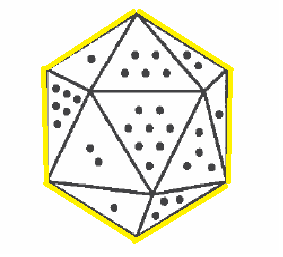
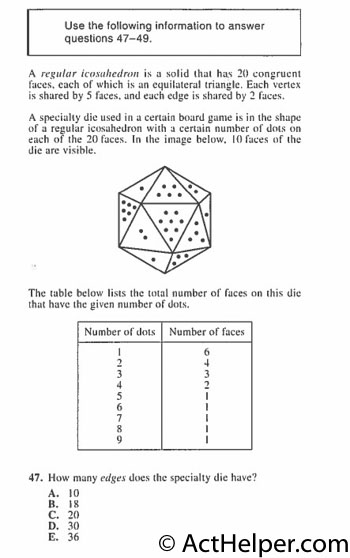
In this image, 10 faces …
Choice G
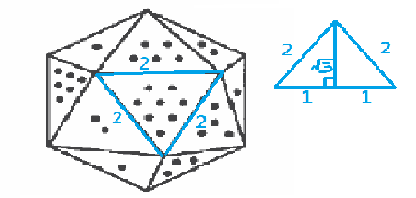
$$\Rightarrow 2\times\sqrt{3}\times\frac{1}{2}=\sqrt{3} $$
Choice C
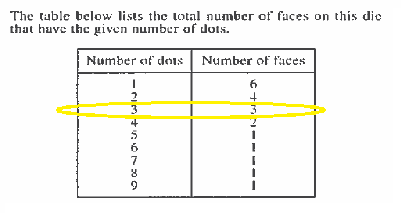
$$P(3\ dots)=\frac{3}{20}=0.15$$
Choice J
$$1-\frac{4}{24}=\frac{20}{24}=\frac{5}{6}$$
Choice D
$$\frac{20\times74+25\times92}{20+25}$$ $$=\frac{1480+2300}{45}=84$$
Choice H
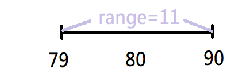
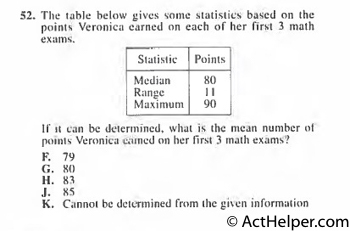
$$\Rightarrow \frac{(79+80+91)}{3}$$ $$=\frac{249}{3}=83$$
Choice C
$$c_{30}^3=\frac{30!}{3!(30-3)!}$$ $$=\frac{30!}{3!(27)!}$$ $$=\frac{30\times29\times28}{3\times2\times1}$$
Choice H
They both live here for …
Choice E
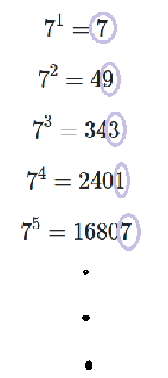
$$126\div4=31...2 $$
Choice J
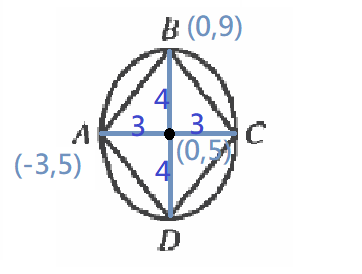
Choice E
3,5,6 are factors of 90 …
Choice F
$$7.5\div.045=16...0.3$$ $$100\div16=6...4$$ $$4\times0.45=1.8$$
Choice E
$$=\frac{3}{(x+3)(x-3)}+\frac{6}{(x+6)(x-3)}$$ $$=\frac{3(x+6)}{(x+3)(x-3)(x+6)}+\frac{6(x+3)}{(x+6)(x-3)(x+3)}$$ $$=\frac{3x+18+6x+18}{(x+6)(x-3)(x+3)}$$ $$=\frac{9x+36}{(x+6)(x-3)(x+3)}$$
Choice J
$$x^{\frac{1}{3}} y^{\frac{5}{4}}$$ $$=x^{\frac{1\times4}{3\times4}} y^{\frac{5\times3}{4\times3}}$$ $$=x^{\frac{4}{12}} …