Choice D
$$$59.95\approx$60$$ $$\frac{20}{100}\times$60=$12$$ $$$60 - $12 = $48$$ $$$48\approx.$47.96$$
Choice E
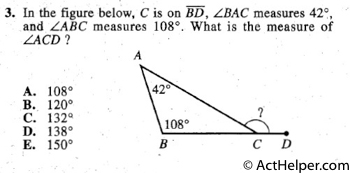
$$\angle ACB = 180°- \angle ABC - \angle BAC = 180° - 108° - 42° = 30°$$ $$\angle ACD = 180° - \angle ACB = 180° - 30° = 150°$$
Choice H
White : 10
Not-white : 3 red + 5 blue = 8
The probability of randomly selecting 1 button that is NOT white
$$= \frac{8}{10+8}=\frac{8}{18}=\frac{4}{9}$$Choice K
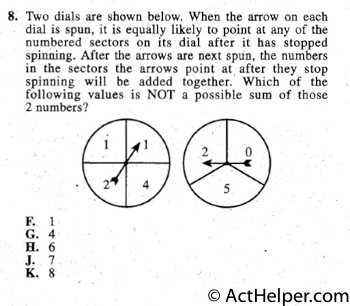
1: 1+0=1
4: 2+2=4
6: 4+2=6
7: 5+2=7
8 is NOT a possible sum of those 2 numbers
Choice B
$$\widetilde{13}=6.6 miles$$ $$\widetilde{23}=4.5 miles$$ $$\widetilde{25}=9.7 miles$$ $$\widetilde{12}=\widetilde{13}-\widetilde{23}=6.6-4.5=2.1 miles$$ $$\widetilde{15}=\widetilde{12}+\widetilde{25}=2.1+9.7=11.8 miles$$
Choice D
N: the maximum number of bats that can be produced by the company
$$ $3,500+$2\times N =$15000 $$ $$ $2\times N = $11500 $$ $$N=5750 $$Choice G
$$3x+2=4$$ $$\Rightarrow 3x=2$$ $$\Rightarrow x=\frac{2}{3}$$ $$2y+6=5$$ $$\Rightarrow 2y=-1$$ $$\Rightarrow y=\frac{-1}{2}$$ $$x+y=\frac{2}{3}+\frac{-1}{2}=\frac{4}{6}+\frac{-3}{6}=\frac{1}{6}$$
Choice C
$$\require{cancel} $$ $$\frac{ 15x ^{2}+25x}{5x}=\frac{\cancel{5}(3x^{2}+5x)}{\cancel{5}x}=\frac{3x^\cancel{2}+5\cancel{x}}{\cancel{x}}=3x+5$$
Choice K
$$ {\displaystyle \left\vert -5\right\vert^{2} =25}$$ $$\Rightarrow\frac{\displaystyle \left\vert -5\right\vert^{2}+(-1)}{(16\div4)\times2-5}=\frac{25-1}{4\times2-5}=\frac{24}{8-5}=\frac{24}{3}=8$$
Choice D
This special savings account will double every 5 years.
$$ \because 40\ years = 5\ years\times 8 $$Therefore, this account will double 8 times.
$$ $2000\times 2^{8}=$2000\times256=$512000 $$Choice F
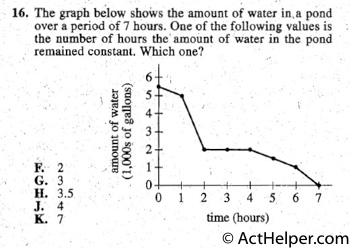
2 hours ~ 4 hours:
the number of hours the amount of water in the pond remained constant.
Choice B
lf it rains in Franklin City on a particular day, the probability that it will rain there the following day is 0.70.
Therefore,
if it rains on a Monday,
the probability that it will NOT rain there the following day is
1 - 0.70 = 0.30
Choice B
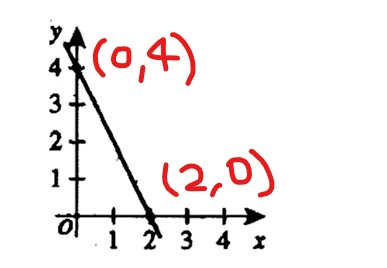
$$Slope=\frac{y-y_{0}}{x-x_{0}}$$ $$\Rightarrow \frac{4-0}{0-2}=-2$$ $$\Rightarrow y=-2x+4$$
Choice D
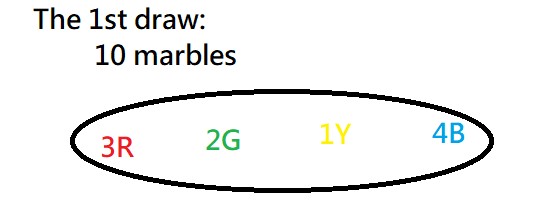
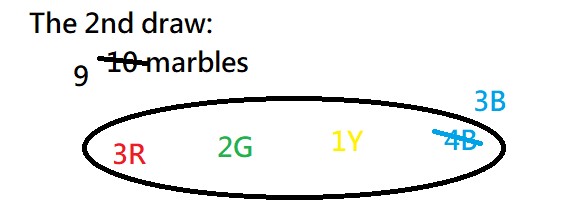
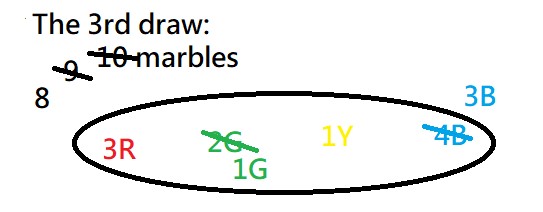
The 1st draw: a blue …
Choice K
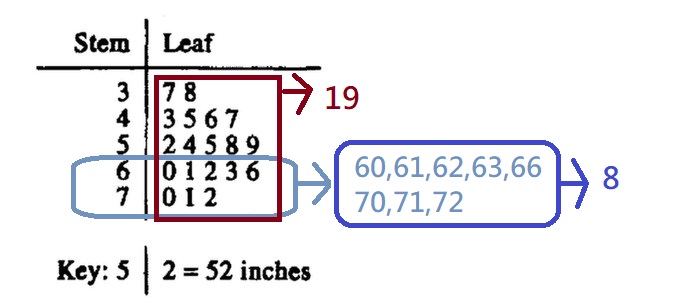
At least 60 inches ⇒ …
Choice C
$$f(x)=5-3x $$ $$\left\{-1,0,2\right\} $$ $$f(-1)=5-3(-1)=8$$ …
Choice F
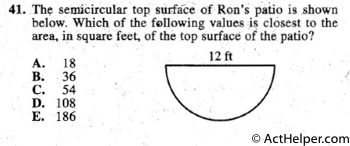
$$100 cubic feet =15\times 1\frac{1}{3}\times …
Choice C
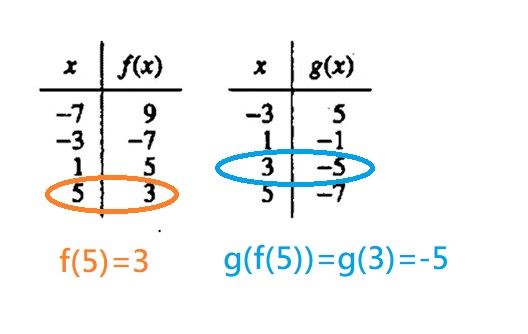
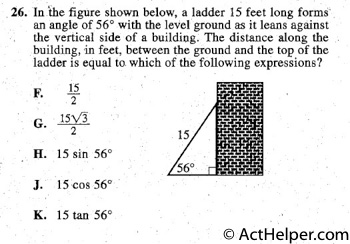
Choice H
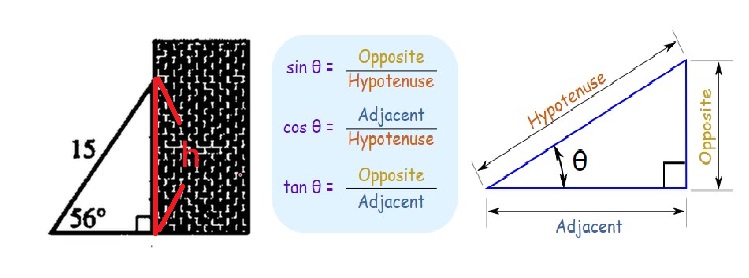
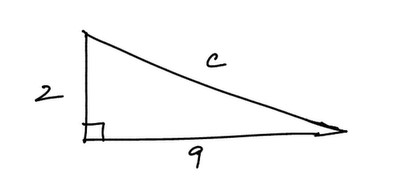
$$\frac{h}{15}=\sin56°$$ $$h=15 \sin56°$$
Choice C
The amount of iodine-131 remaining …
Choice F
$$\sqrt[4]{256x^{16}}=(256x^{16})^{\frac{1}{4}}$$ $$=256^{\frac{1}{4}}\times (x^{16})^{\frac{1}{4}}$$ $$=(16^{2})^{\frac{1}{4}}\times x^{4}$$ …
Choice C

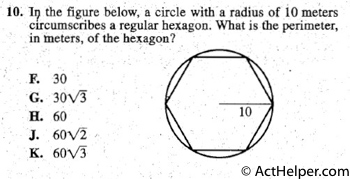
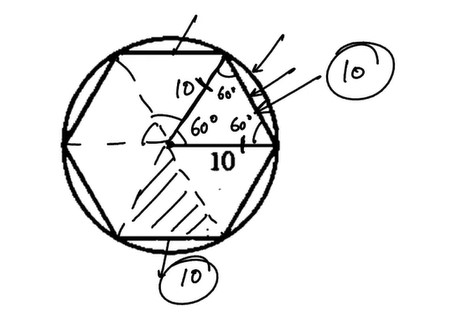
The formula for the circumference …
Choice G
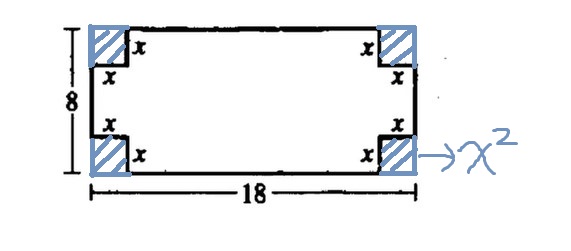
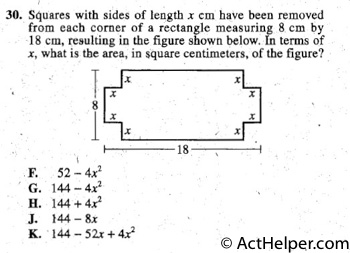
$$Area= 8\times18-4\times x^{2} =144-x^{2}$$
Choice E
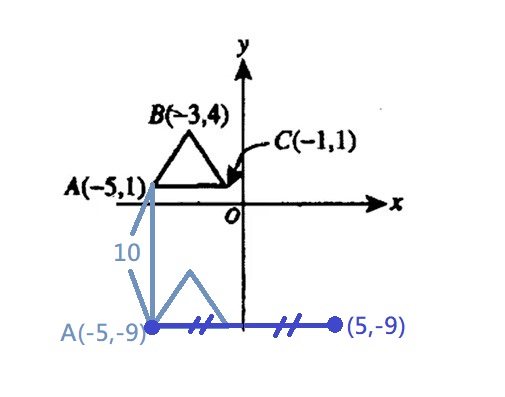
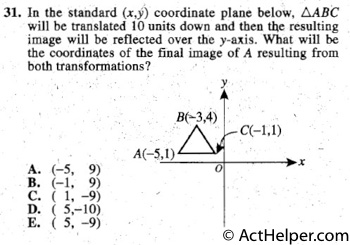
A(-5,1-10)=A(-5,-9)
Choice J
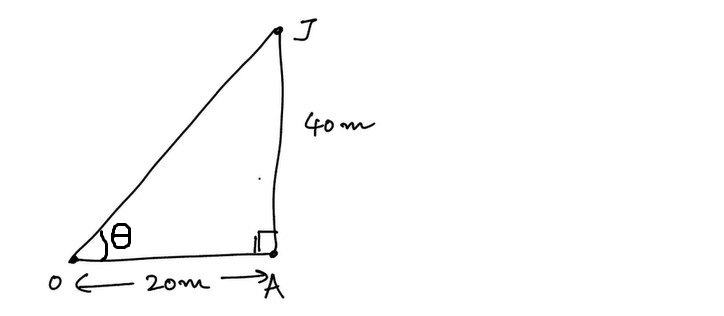
$$\tan\theta=\frac{20}{40}$$ $$\Rightarrow\theta=\tan^{-1}\frac{20}{40}$$
Choice D
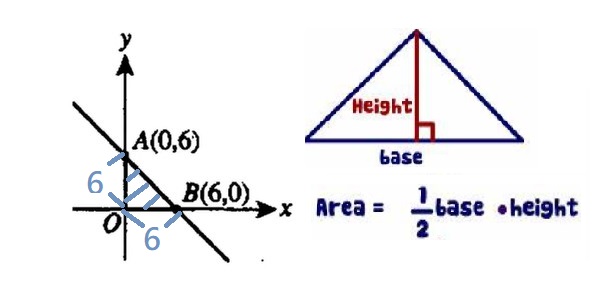
$$ Area = \frac{1}{2}\times6\times6=18 $$
Choice G
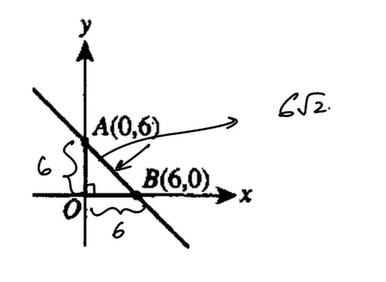
Choice A
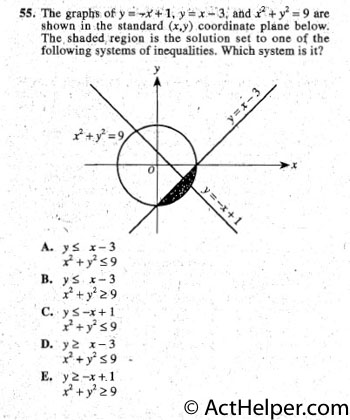
$$\because y=mx+b$$ $$A(0,6)\Rightarrow6=0+b\Rightarrow b=6$$ $$B(6,0)\Rightarrow0=m\cdot6+6\Rightarrow …
Choice K
$$\frac{9}{5}=1.8 $$ $$1.\overline{8}=1.88888... $$ $$1.08=1.08$$ …
Choice A
$$\frac{6\times3+8\times2+2\times1+4\times0}{20}$$ $$=\frac{18+16+2+0}{20}$$ $$=\frac{36}{20}$$ $$=\frac{9}{5}=1.8$$
Choice G
$$(F)14+(\frac{-1}{40})=14-(\frac{1}{40})$$ $$(G)14-(\frac{-1}{40})=14+\frac{1}{40}$$ $$(H)14\div(\frac{-1}{40})=14\times(-40)=-560$$ $$(J)14\times(\frac{-1}{40})=\frac{-14}{40}$$ $$(K)\frac{14+\frac{-1}{40}}{2}=7+\frac{-1}{80}$$
Choice E
$$H=0.75\times(200-A)$$
Choice J
t=-0.0066a+15
t : degrees Celsius …
Choice C
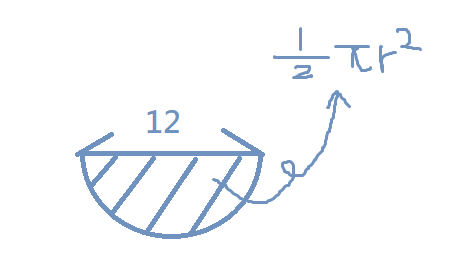
$$The\ formula\ for\ the\ area\ …
Choice J
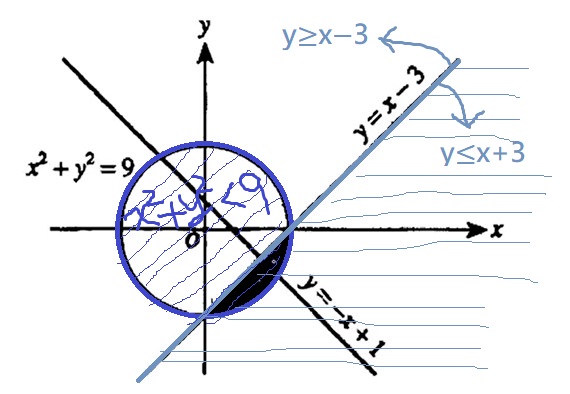
$$(x-h)^{2}+(y-k)^{2}=r^{2}$$ $$(h,k)=(1,-4)$$ $$r=5$$ $$\Rightarrow (x-1)^{2}+(y+4)^{2}=5^{2}$$
Choice D
$$5= 1\times5 \Rightarrow1,5$$ $$6=1\times6, 2\times3 …
Choice K
$$49^{a}= (7^{2})^{a}=7 $$ $$\Rightarrow a=\frac{1}{2}$$ …
Choice A
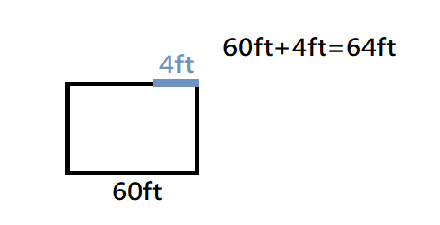
$$(A)16\times16=256,\ 16\times4=64$$ $$(B)17\times17=289,\ 17\times4=68\gt64$$ $$(C)14\times16=224\lt256,\ …
Choice J
$$\frac{3}{5}-(\frac{-1}{3})$$ $$=\frac{9}{15}+\frac{5}{15}=\frac{14}{15}$$ $$\frac{14}{15}=1-\frac{1}{15} \Rightarrow \frac{14}{15} …
Choice B
$$a_{1}=10 $$ $$a_{n}=a_{n-1}+5 $$ $$\Rightarrow …
Choice F
$$P(A\ and\ B)=P(A)\times P(B) $$ …
Choice E
$$x^{4}+21x^{2}-100=0 $$ $$Let\ x^{2}=a, $$ …
Choice F
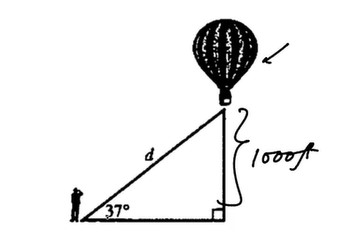
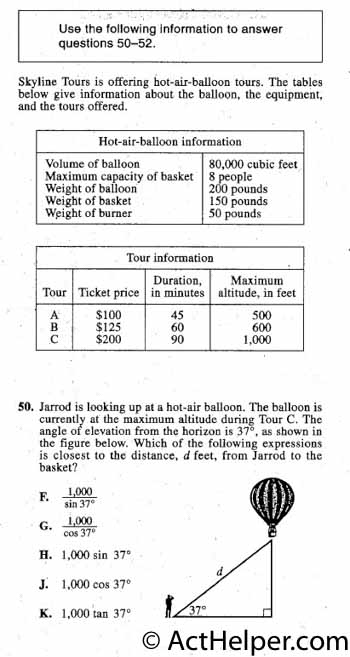
$$\sin37°=\frac{1000}{d}$$ $$\Rightarrow d=\frac{1000}{\sin37°}$$
Choice E
$5000 in 1 day
Tickets …
Choice G
$$Speed=\frac{Distance}{Time}$$ $$6\ miles\div \frac{45}{60}\ hours …
Choice A
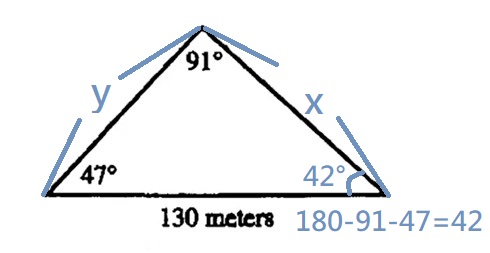
$$\frac{perimeter}{4}=\frac{130+x+y}{4}$$ $$\frac{x}{\sin47°}=\frac{130}{\sin91°}=\frac{y}{\sin42°}$$ $$x=\frac{130\sin47°}{\sin91°}$$ $$y=\frac{130\sin42°}{\sin91°}$$ $$\Rightarrow\frac{perimeter}{4}=\frac{130+\frac{130\sin47°}{\sin91°}+\frac{130\sin42°}{\sin91°}}{4}$$
Choice G
$$21=3\times7 $$ $$22=2\times11 $$ $$23=23 …
Choice A
Choice J
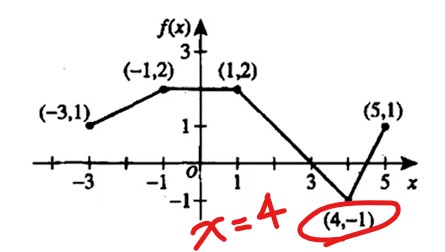
$$g(x)=-[f(x)-3]$$ $$g(4)=-[f(4)-3]$$ $$f(4)=-1$$ $$\Rightarrow g(4)=-[(-1)-3]=4$$
Choice D
$$\require{cancel} $$ $$\frac{a}{b}=\frac{6}{1}\Rightarrow a=6b $$ …
Choice F
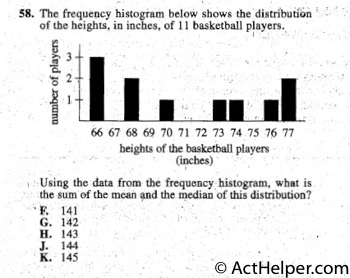
$$Median=70 $$ $$Mean=\frac{66\times3+68\times2+70+73+74+76+77\times2}{11}=71 $$ $$Median+Mean=141$$
Choice A
Definition of y-intercept: the y-coordinate …
Choice K

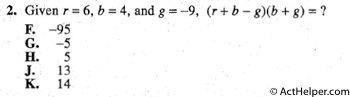







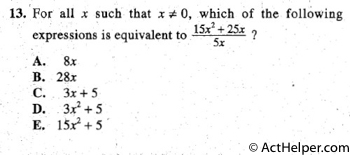

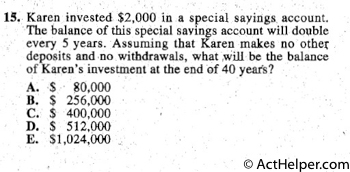



























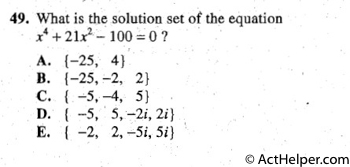



![56. The function f (x) is shown below with several points
labeled. Another function, g(x), is defined such that
g(x) = --[f(x) - 3]. What is g(4)?](/media/questions/b02_math_q56.jpg)


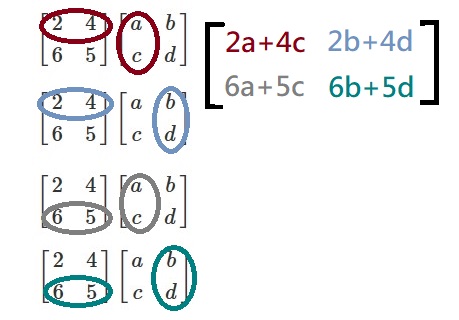
![60. What is the matrix product [2 4 ] [a b] ? _](/media/questions/b02_math_q60.jpg)