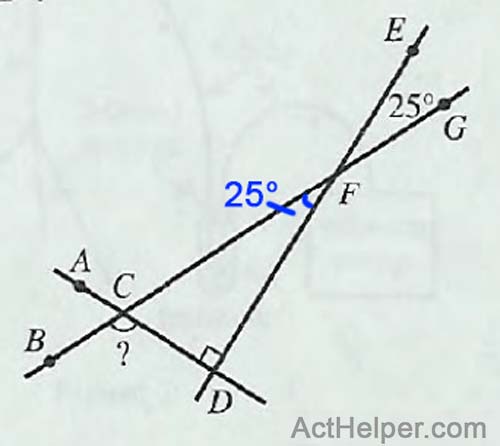
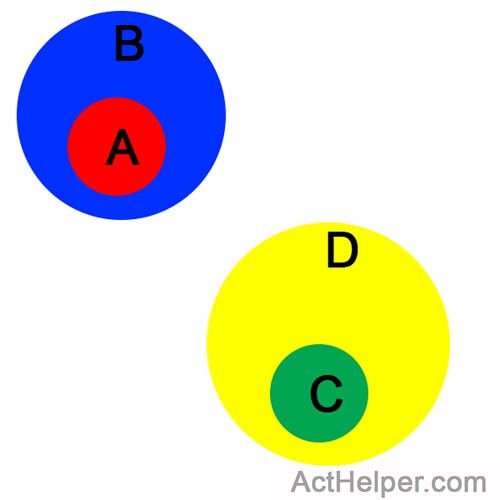
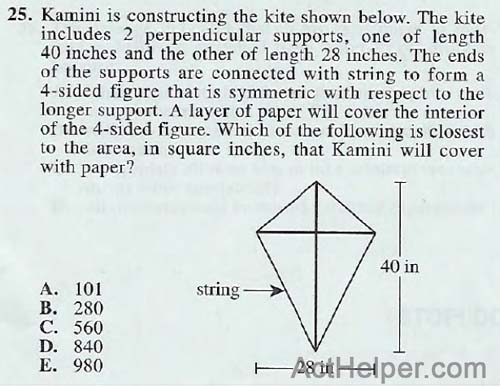
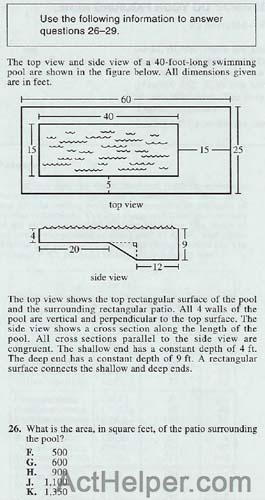
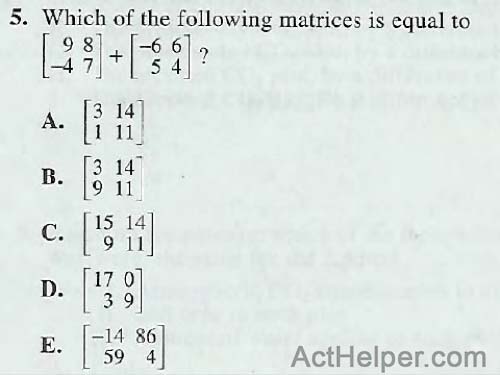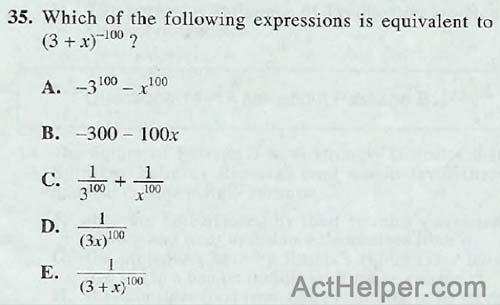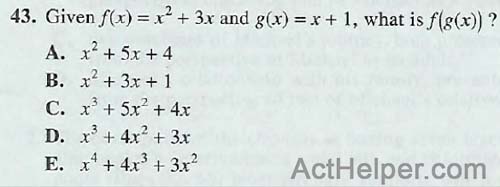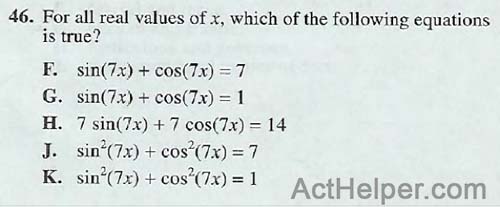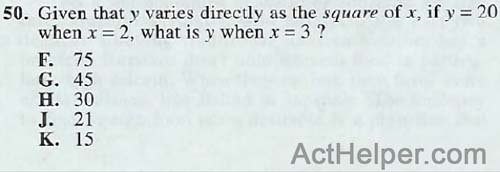Choice C
Shantiel travelled for 18 hours from 9am to 3am the next day. \begin{align*} s=\frac{648}{18}=36 \end{align*}
Choice A
\begin{align*} \begin{bmatrix} 9&8\\ -4&7\\ \end{bmatrix}+ \begin{bmatrix} -6&6\\ 5&4\\ \end{bmatrix}= \begin{bmatrix} 9-6&8+6\\ -4+5&7+4\\ \end{bmatrix}= \begin{bmatrix} 3&14\\ 1&11\\ \end{bmatrix} \end{align*}
Choice H
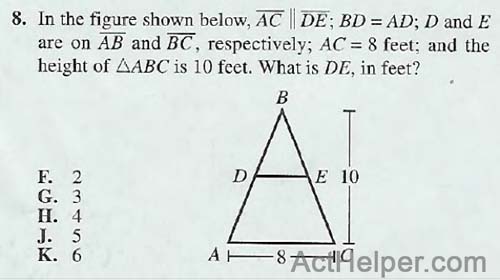
\begin{align*} AC \parallel DE , \ BD=AD\\ \Rightarrow DE=\frac{AC}{2}=\frac{8}{2}=4 \end{align*}
Choice B
\begin{align*} n=22000\times \frac{337}{500}=14828\approx 14830 \end{align*}
Choice G
\begin{align*} Total \ payment=400+300\times48=14800 \\ Difference=14800-13400=1400 \end{align*}
Choice A
\begin{align*} 4x+7y=9 \\ \Rightarrow 7y=-4x+9 \\ \Rightarrow y=-\frac {4}{7}x+\frac {9}{7} \\ \Rightarrow Slope =-\frac {4}{7} \end{align*}
Choice C
\begin{align*} x^2+x-30=0\\ \Rightarrow (x+6)(x-5)=0\\ \Rightarrow x=-6,\ 5\\ \Rightarrow sum \ of two \ solutions=-6+5=-1 \end{align*}
Choice F
\begin{align*} d=4\\ \Rightarrow r=\frac{d}{2}=\frac{4}{2}=2\\ \Rightarrow v=\frac{4\pi r^3}{3}=\frac{4\pi 2^3}{3}=\frac{32}{3} \pi \end{align*}
Choice C
\begin{align*} 10=\sqrt{100} \ which\ is\ greater\ than\ \sqrt{85} \\ 9=\sqrt{81} \ which\ is\ less\ than\ \sqrt{85} \end{align*}
Choice K
\begin{align*} p=\frac{8+7}{25}=\frac{15}{25}=\frac{3}{5}=60\% \end{align*}
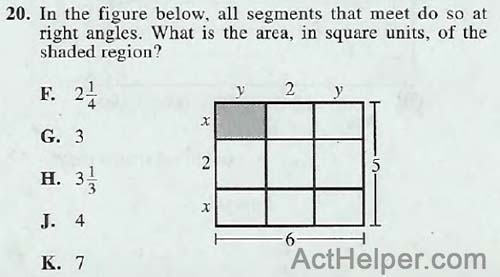
Choice G
\begin{align*} x+2+x=5 \Rightarrow x=\frac{3}{2}\\ y+2+y=6 \Rightarrow y=2\\ \Rightarrow shaded \ area=xy=\frac{3}{2}\times 2=3 \end{align*}
Choice D
\begin{align*} 5x+(3x+30)+(2x+10)=100\Rightarrow x=6\\ 3x+30=3\times 6+30=48 …
Choice J
\begin{align*} ^nP_k=\frac{n!}{(n-k)!} \end{align*} \begin{align*} ^6P_6=\frac{6!}{(6-6)!} …
Choice E
\begin{align*} 2+200\%\cdot1=2+2=4=400\%\cdot1 \end{align*}
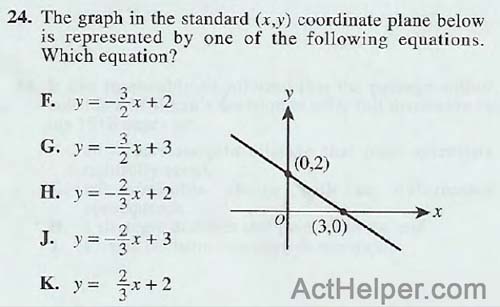
Choice H
\begin{align*} Choice \ H: y=f(x)=-\frac{2}{3}\cdot …
Choice C
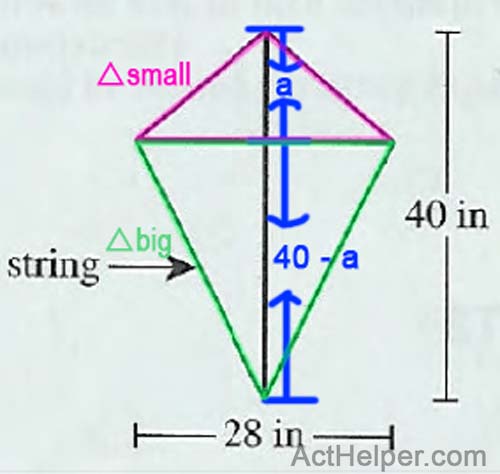
\begin{align*} & Let\ a\ be\ …
Choice H
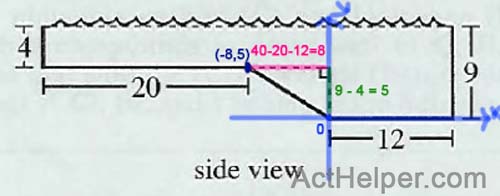
\begin{align*} Area \ of \ …
Choice D
\begin{align*} cost=12\times(60+25+60+25)=2040 \end{align*}
Choice J
\begin{align*} 1 \ full \ …
Choice B
\begin{align*} k=\frac{0-5}{0-(-8)}=-\frac{5}{8}=-0.625\approx-0.63 \end{align*}
Choice K
\begin{align*} cost \ of \ …
Choice C
\begin{align*} \frac{5 \ feet \ …
Choice H
\begin{align*} 18+18\times \frac{2}{3}+18\times \frac{2}{3}\times \frac{2}{3}+18\times …
Choice B
\begin{align*} \end{align*}
Choice K
\begin{align*} increase \ in \ …
Choice E
One need to know that …
Choice G
\begin{align*} 2x-6=0\\ \Rightarrow x=3 \end{align*}
Choice C
\begin{align*} xy=0 \Rightarrow x=0 \ …
Choice F
\begin{align*} v=\frac{3.7 \ km}{15 \ …
Choice A
\begin{align*} 2.5 \ million = …
Choice K
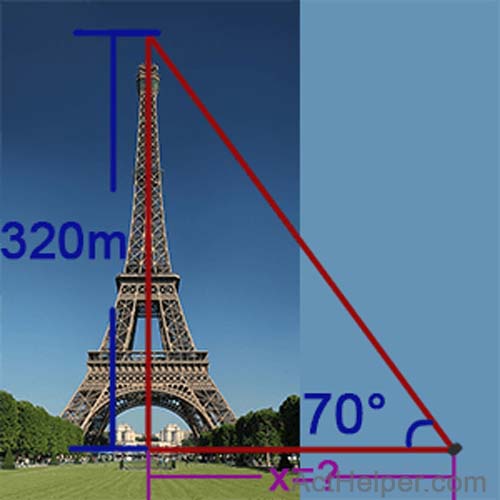
\begin{align*} \tan 70°=\frac{320}{x}\Rightarrow x=\frac{320}{\tan 70°} …
Choice E
\begin{align*} a-2=6 \Rightarrow a=9\\ 3+b=-6\Rightarrow …
Choice F
\begin{align*} c=10b^3+50 \\ \Rightarrow c-50=10b^3\\ …
Choice A
\begin{align*} f(g(x))=(g(x))^2+3g(x)=(x+1)^2+3(x+1)\\ =x^2+2x+1+3x+3 \\ =x^2+5x+4 …
Choice J
\begin{align*} d_1=12 \Rightarrow 2\pi r_1=12\Rightarrow …
Choice D
The first 6 prime numbers …
Choice K
One need to know that …
Choice A
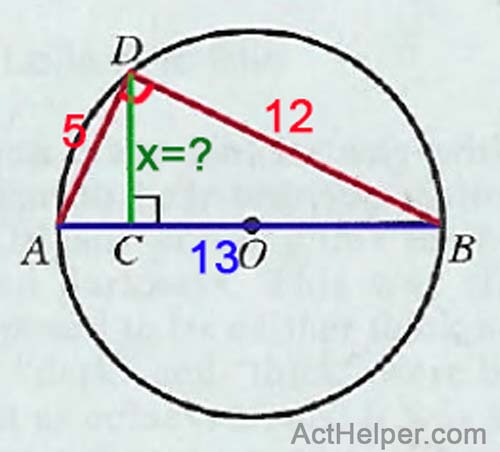
\begin{align*} 13x=5\times12 \Rightarrow x=\frac{60}{13} \end{align*}
Choice K
\begin{align*} a>0 \Rightarrow |a|=a …
Choice D
\begin{align*} x < y \Rightarrow x+y<2y \ (1)\\ y<4 \Rightarrow 2y<8 \ (2)\\ (1)+(2) \Rightarrow x+y<8 \\ (x+y)_{greatest \ possible \ integer}=7 \end{align*}
Choice G
\begin{align*} y=kx^2\\ 20=4k\Rightarrow k=5 \\ …
Choice D
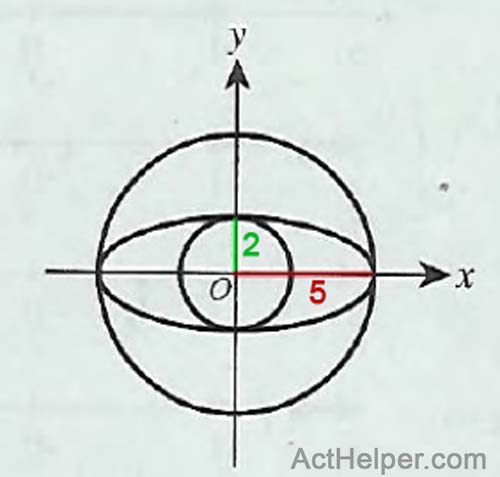
\begin{align*} \frac{(x-h)^2}{a^2}+\frac{(y-h)^2}{b^2}=1 \end{align*}
This is …
Choice H
The sum of the other …
Choice B
The sum positive integers of …
Choice G
\begin{align*} average \ rate =\frac{2\times\frac{10}{60}+3\times\frac{5}{60}}{\frac{10}{60}+\frac{5}{60}}=\frac{7}{3} …
Choice D
\begin{align*} A=5n\\ B=7n=4m\Rightarrow n=\frac{4m}{7}\\ C=3m\Rightarrow …
Choice K
\begin{align*} x^\frac{2}{3}=\sqrt[3]{x^2} \end{align*}
Choice B
\begin{align*} 1.25a\times0.9b=1.125ab \end{align*}
Choice F
When 3 and 4, or, …
Choice D
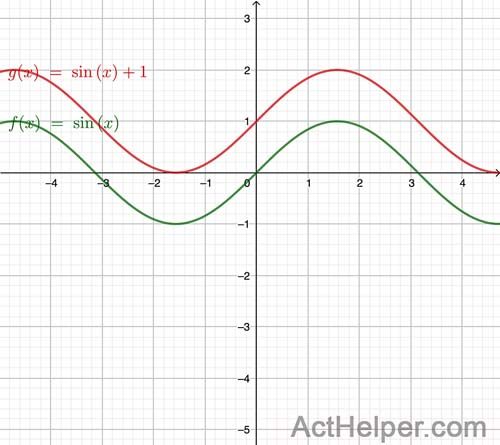
\begin{align*} \end{align*}
Choice G
\begin{align*} 1 \ yard = …