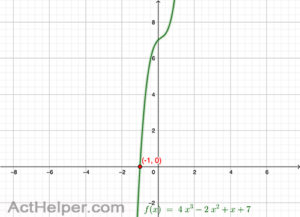
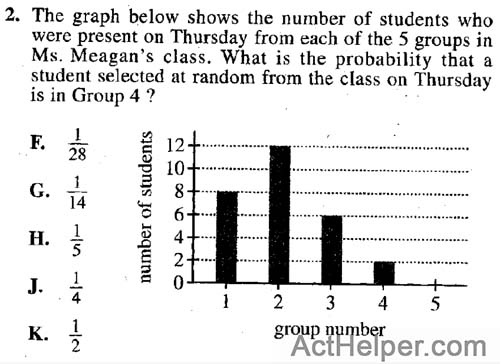
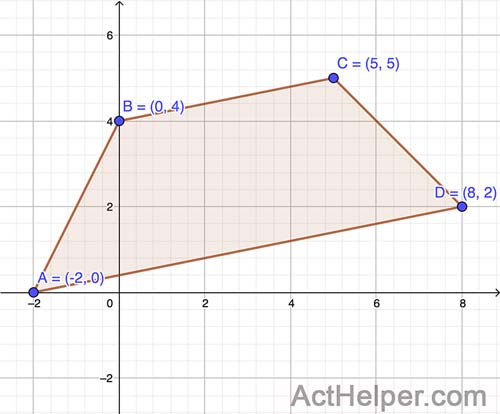
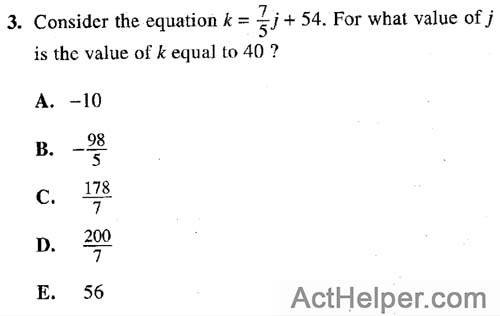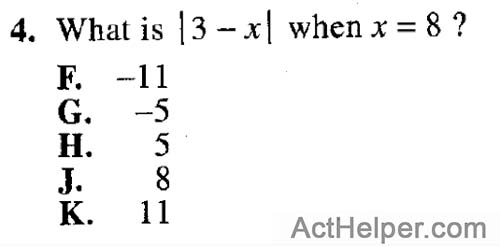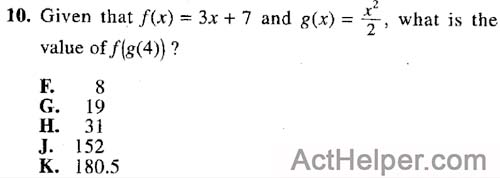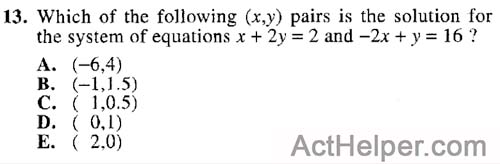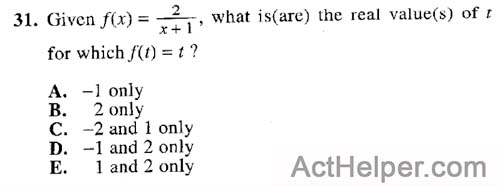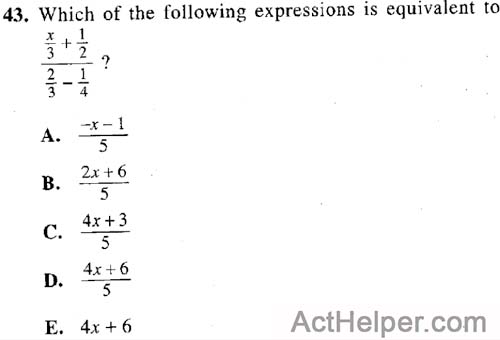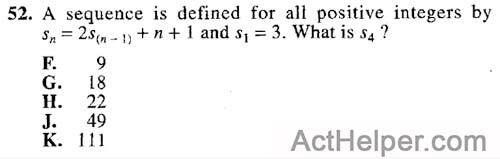Choice J
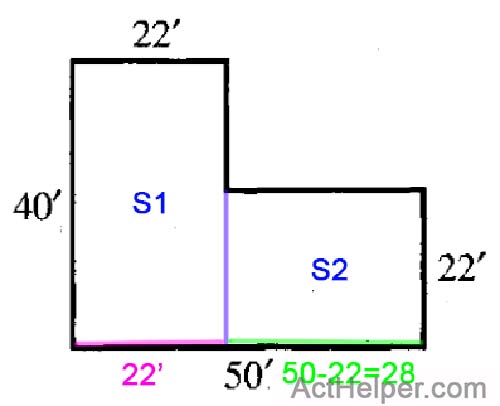
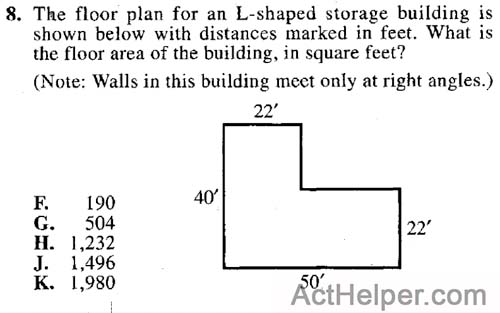
$$S_1=22\times40=880\\$$ $$S_2=22\times28=616\\$$ $$\Rightarrow S_1+S_2=1496$$
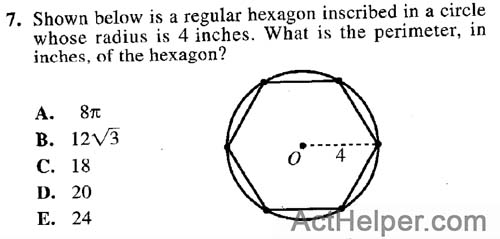
Choice H
$$g(4)=\frac{4^2}{2}=\frac{16}{2}=8\\$$$$\Rightarrow f(g(4))=f(8)=3\times 8+7=31$$
Choice G
$$3x+8y=5$$ $$\Rightarrow 8y=-3x+5 $$ $$\Rightarrow y=-\frac{3}{8}x+\frac{5}{8}$$
Choice A
$$x+2y=2\ (given)\Rightarrow x=2-2y \ (a)\\$$ $$-2x+y=16 \ (given) \ and \ (a) \Rightarrow -2(2-2y)+y=16\Rightarrow y=4 \\$$ $$\Rightarrow x= 2-2\times4=-6$$
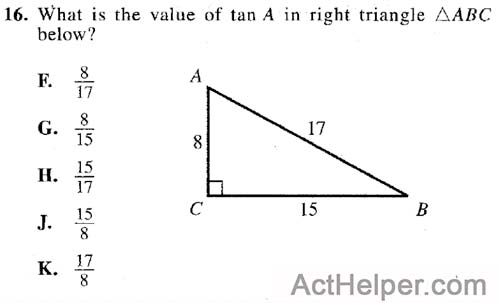
Choice K
$$\frac{x \ miles}{2\frac{3}{4}inches}=\frac{16\ miles}{\frac{1}{4}\ inches}\\$$ $$\Rightarrow \frac{x}{\frac{11}{4}}=\frac{16}{\frac{1}{4}}\\$$ $$\Rightarrow \frac{x}{11}=\frac{16}{1}\\$$ $$\Rightarrow x=16\times11=176 \ miles$$
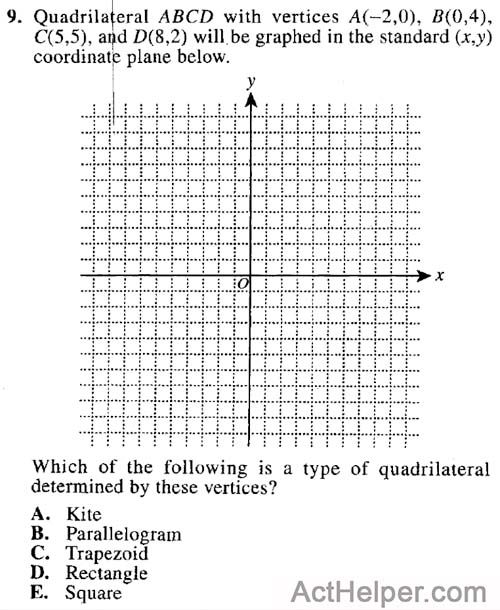
Choice E
$$4\begin{bmatrix}-1&2\\0&-4\\ \end{bmatrix}=\begin{bmatrix}-1\times4&2\times4\\0\times4&-4\times4\\ \end{bmatrix}=\begin{bmatrix}-4&8\\0&-16\\ \end{bmatrix}$$
Choice F
$$Let \ the \ linear \ function \ be \ y=kx+b \\$$ $$\Rightarrow 2=5k+b\\$$ $$6=15k+b\\$$ $$\Rightarrow k=\frac{2}{5},\ b=0\\$$ $$y=\frac{2}{5}x$$
Choice C
When at noon (12pm), the …
Choice K
Let the points on the …
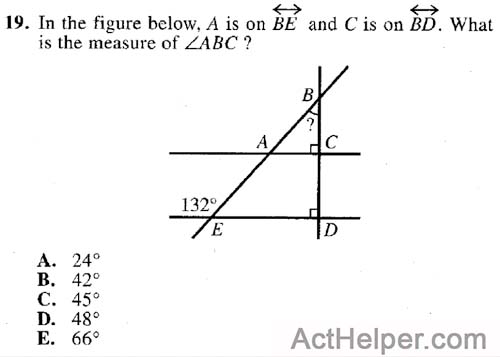
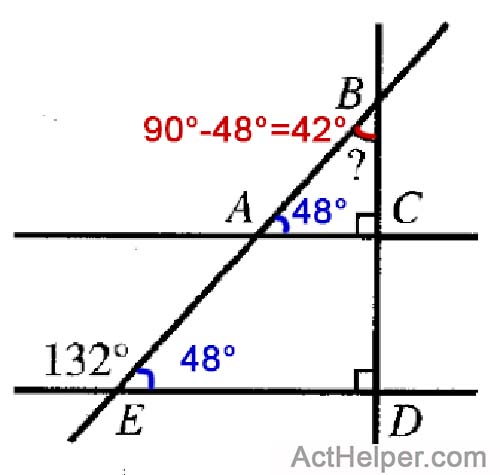
2017 December(A10) Math Question 23
Algebraic & Function Expressions
- Triangles, Squares, Rectangles, Circles
Choice A
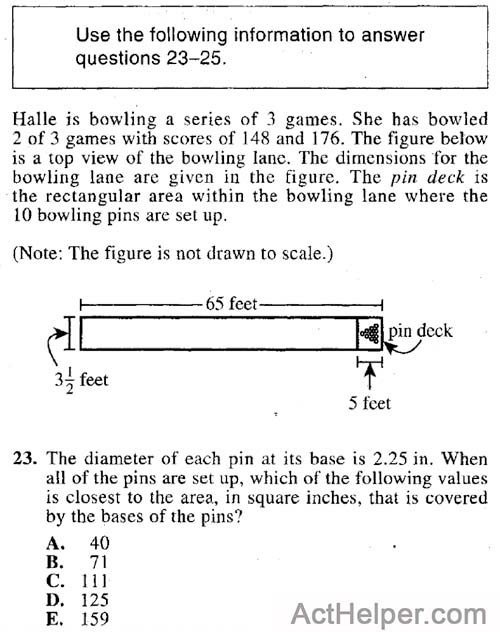
The area of 10 pins …
Choice G
$$\frac{65\times3\frac{1}{2}}{5\times3\frac{1}{2}}=\frac{13}{1} $$
Choice D
$$\frac{148+176+x}{3}=172 \\ $$ $$\Rightarrow x=192 …
Choice F
$$l=3w\\$$ $$ S=l\cdot w=3w^2=300 \\$$ …
Choice C
$$16+16+2x=96 \\$$ $$ \Rightarrow x=32 …
Choice H
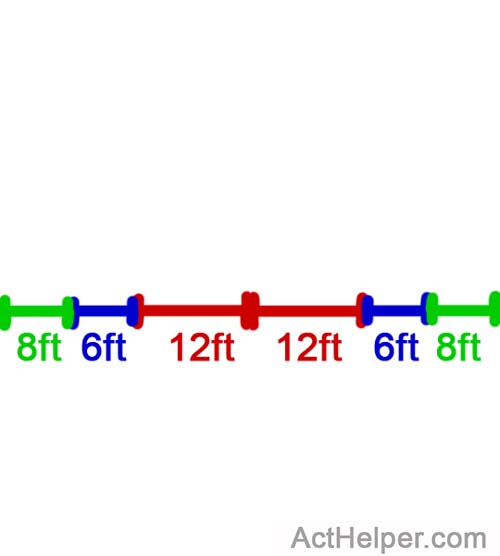
8+6+12+8+6+12=52
Choice A
$$2500\times \frac{4}{10}\times \frac{3}{8}=375$$
Choice H
$$\sin^2 \theta+\cos^2\theta=1 \\$$ $$\Rightarrow \cos\theta=\pm …
Choice C
$$f(t)=\frac {2}{t+1}=t \\ $$ $$\Rightarrow …
Choice J
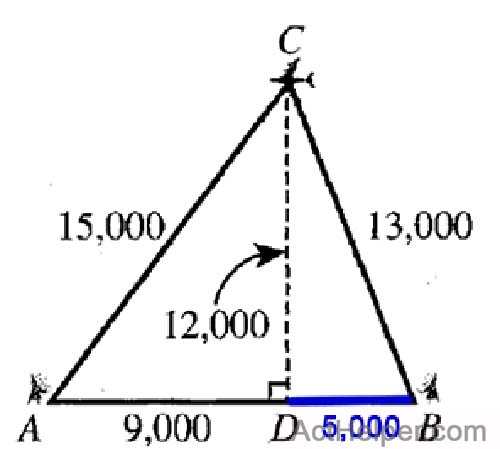
$$ BD=\sqrt{BC^2-CD^2}=\sqrt{13000^2-12000^2}=5000\\$$ $$\Rightarrow AB=AD+DB=9000+5000=14000$$
Choice C
Choice G
$$ t=\frac{9000}{300}=30$$
Choice A
B is apparently decreasing. C …
2017 December(A10) Math Question 36
Ratios, Proportions, Percentages, Fractions
- Triangles, Squares, Rectangles, Circles

Choice G
$$\frac{3}{4}\times 4 \times w=50\% \times …
Choice E
$$ x+6=2(x+3)-x \\$$ $$ \Rightarrow …
2017 December(A10) Math Question 38
Exponents, Radicals, & Scientific Notation
- Triangles, Squares, Rectangles, Circles

Choice J
Let L be the length …
Choice C
The range and the mean …
Choice K
Ruben completed $$1-\frac{2}{5}-\frac{1}{3}=\frac{4}{15}$$ The total …
Choice C
$$\frac{(2a^{-1}\sqrt{b})^4}{ab^{-3}}=\frac{2^4a^{-4}(\sqrt{b})^4}{ab^{-3}}=\frac{16b^2}{a^5b^{-3}}=\frac{16b^5}{a^5}$$
Choice G
There is only one correct …
Choice D
$$\frac{\frac{x}{3}+\frac{1}{2}}{\frac{2}{3}-\frac{1}{4}}=\frac{\frac{2x+3}{6}}{\frac{8-3}{12}}=\frac{\frac{2x+3}{6}}{\frac{5}{12}}=\frac{2x+3}{6}\cdot \frac{12}{5}=\frac{(2x+3)\cdot2}{5}=\frac{4x+6}{5}$$
Choice K
10×10×10×26×26×26=17576000
Choice A
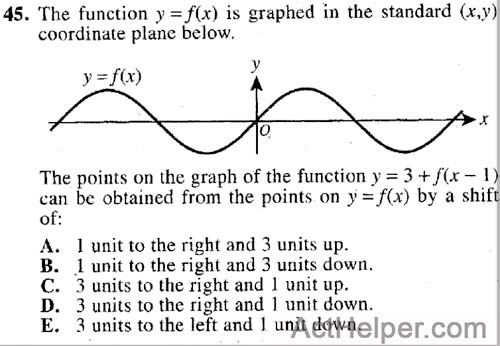
The function is moved to …
Choice K
$$ x=5^{-2}=\frac{1}{25} $$
Choice D
$$\frac{1}{5}=\frac{2}{10} \\$$ $$ \frac{1}{3}=\frac{2}{6}$$ The …
Choice F
The effect of a number …
2017 December(A10) Math Question 49
Ratios, Proportions, Percentages, Fractions
- Advanced sin, cos, tan functions
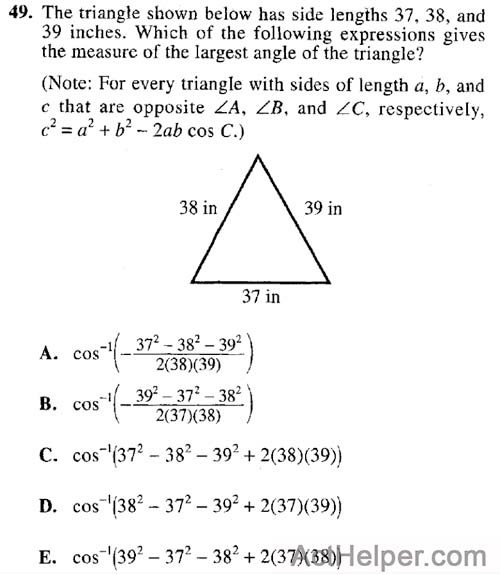
Choice B
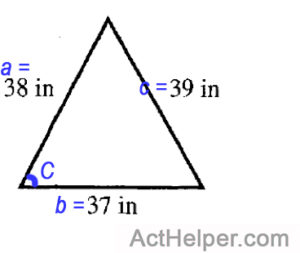
$$ 39^2=38^2+37^2-2\times38\times37cos\ C \\$$ $$ …
Choice K
$$ x+2=\frac{4x+(x+s)}{5} \\$$ $$ \Rightarrow …
Choice D
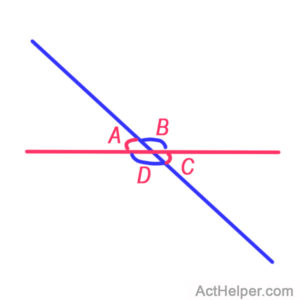
As seen from the diagram, …
Choice J
$$ s_2=2s_1+3=2\times3+3=9 \\$$ $$ s_3=2s_2+4=2\times9+4=22 …
Choice E
Let a be -2: $$ …
Choice J
$$ Expected \ value \ …
Choice B
Since x, y and z …
Choice G
$$ 24=\frac{42+3+11+27+x}{5} \Rightarrow x=37 \\$$ …
Choice A
For A: $$ \\2\times(W+L)=48 \Rightarrow …
Choice J
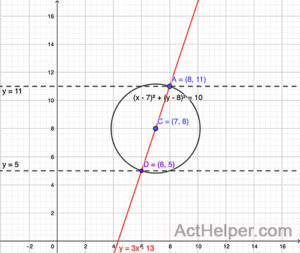
$$(x-7)^2+(y-8)^2=10 \\ $$ $$y=11 \\$$ …
Choice D
$$V_0=30\times25\times5\\$$ $$ V_1=30\times 110\%\times 25\times110\%\times5=(110\%)^2\times30\times25\times5=(110\%)^2\times …
Choice K