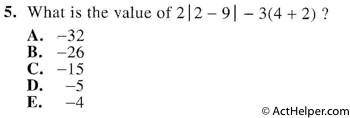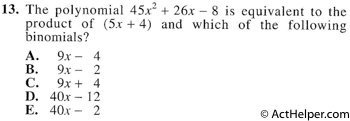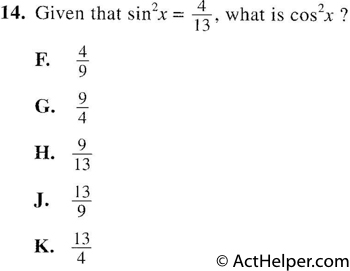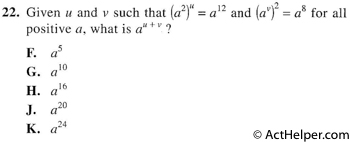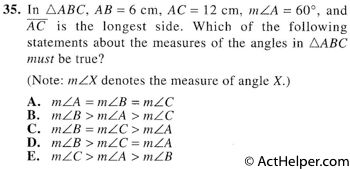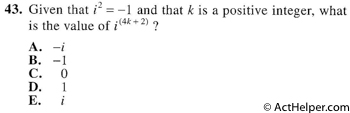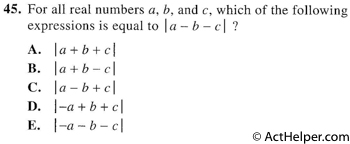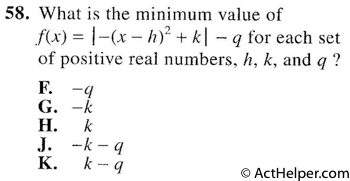Choice C
The number of members who are not officers is 32-5=27.
Luis is one of the 27 members who are not officers. Therefore the probability that he will be chosen is\(\frac{1}{27}\).
Choice K
Since the two triangles are congruent. The following must be true: $$\angle A\cong\angle D\\$$ $$\angle B\cong\angle E \\$$ $$\angle C\cong\angle F\\$$ $$\overline{AB}\cong\overline{DE}\\$$ $$\overline{BC}\cong\overline{EF}\\$$ $$\overline{AC}\cong\overline{DF} $$
Choice C
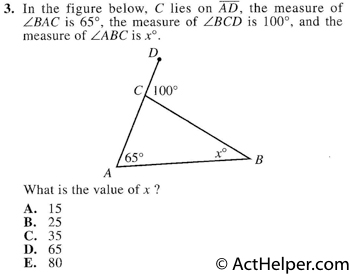
$$\angle BCD+\angle BCA = 180°$$ $$\Rightarrow\angle BCA=180°-100°=80°$$ $$\angle CAB+\angle ABC+\angle BCA=180°$$ $$\Rightarrow 65°+X°+80°=180°$$ $$\Rightarrow X°=35°$$
Choice E
$$ \begin{align} 2|2-9|-3(4+2) & = 2|-7|-3(6) \\ & = 2\cdot7-3\cdot6 \\ & = 14-18 \\ & = -4 \end{align} $$
Choice G
$$ \left\{ \begin{aligned} -2x+y &=2 \\ x+y&=5 \end{aligned} \right. \ \ \Rightarrow\ \ \left\{ \begin{aligned} x &=1 \\ y&=4 \end{aligned} \right. \ \ \Rightarrow\ \ Point \ of\ intersection\ is\ (1,4) $$
Choice C
$$Assessed\ value=$56,000 \times \frac{3}{4}=$42,000\\$$ $$\Rightarrow Yearly\ tax=$3 \times\frac{$42,000}{$100}=$1,260$$
Choice C
Let the number of month be m. $$$75+$65\cdot m=$495\\ \Rightarrow m = 6.46\approx7$$
Choice F
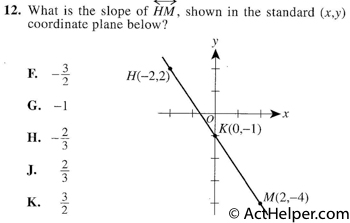
$$Slope\ of\ \overleftrightarrow{HM} = \frac{y_2-y_1}{x_2-x_1} =\frac{-4-2}{2-(-2)} =\frac{-6}{4}=-\frac{3}{2}$$
Choice B
The questions asks what the ( ? ) should be in: $$45x^2+26x-8=(5x+4)(\quad?\quad)$$ To solve for the ( ? ), we need to perform the following: $$ \begin{pmatrix}5&4\\\color{red}{\frac{45}{5}}&\color{red}{\frac{-8}{4}}\\ \end{pmatrix} \Rightarrow \begin{pmatrix}5&4\\\color{red}{9}&\color{red}{-2}\\ \end{pmatrix}\\$$ $$\Rightarrow (\quad?\quad) = (9x-2)$$
Choice H
We know that $$sin^2x\ + cos^2x=1\\$$ $$\Rightarrow cos^2x=1-sin^2x=1-\frac{4}{13}=\frac{9}{13}$$
Choice E
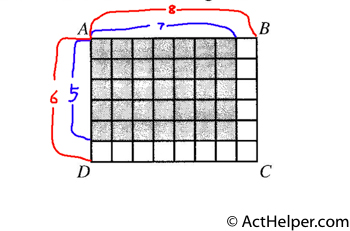
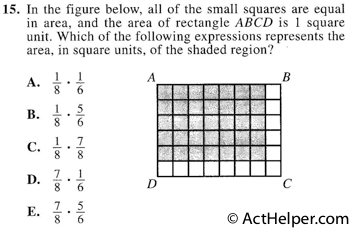
Let each side of small squares be k:
Area of rectangle region = $$6k\cdot8k=1\Rightarrow k^2=\frac{1}{6\cdot8}$$
Therefore, area of shaded region = $$7k\cdot5k = 7\cdot5\cdot k^2=\frac{7\cdot5}{8\cdot6}$$
Choice J
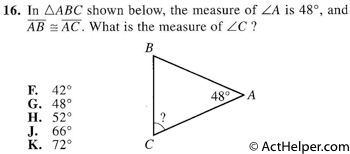
It is given that \(\overline{AB} \cong \overline{AC}\), thus \(\angle B =\angle C\).
Because \(\angle A+\angle B +\angle C = 180^\circ;\ \angle A=48^\circ\), we have: \(\angle C = \frac{180^\circ-48^\circ}{2}=66^\circ\)
Choice B
It is given that $$a_5=39$$. All you need to do is plug in 6 for n: $$\begin{align} a_6 & =a_5+(6-1)^2\\ &=39+25\\ &=64 \end{align}$$
Choice G
Because the line is parallel to the line represented by y = -2x - 4, the line has the same slope -2. Thus we can write the line as: $$y = -2x + b$$ Because the line passes through (0,7): $$7=-2\cdot0 +b\\$$ $$\Rightarrow b=7\\$$ Therefore, the line is: $$y = -2x + 7$$
Choice D
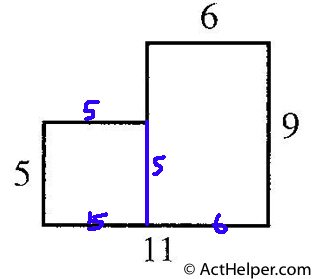
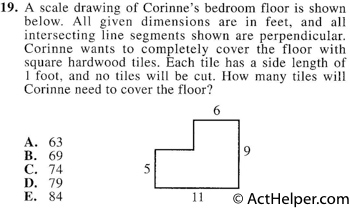
The bedroom floor can be seen as being consisting of one rectangle and a square with lengths as below: Thus the area is $$5\times5+6\times9=79$$. The number of tiles needed is $$\frac{79\ ft^2}{1 \ ft^2}=79$$
Choice F
We are told that the survey accurately predict how the 1,200 resident would respond: $$\require{cancel}\frac {x}{1200}=\frac {12}{60}\\$$ $$\Rightarrow x=\frac {12\times\cancel{1200}20}{\cancel{60}}=240 $$
Choice A
We are told that the …
Choice G
$$(a^2)^u=a^{12}=(a^2)^6\ \Rightarrow u=6\\$$ $$(a^v)^2=a^{8}=(a^4)^2\ \Rightarrow …
Choice B
The shifting rule is that: …
Choice F
$$x=\frac{4a+b}{3}\\$$ $$\Rightarrow 3x=4a+b\\$$ $$\Rightarrow b=3x-4a$$
Choice B
Let the length of the …
Choice J
We need to know \(\pi …
Choice A
Area of rectangle =$$3\sqrt5 \times …
Choice H
11 either divided or multiplied …
Choice D
And, by rearranging the expression, …
Choice E
The key of the committee …
Choice E
To rewrite the expression, we …
Choice F
We need to know: $$1\ …
Choice D
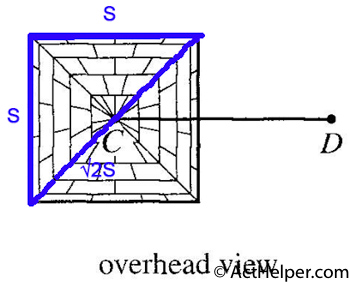
In a square, the lengths …
Choice K
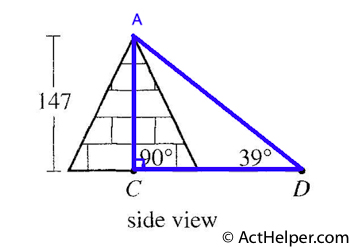
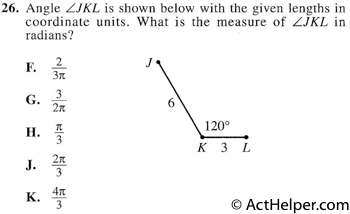
In the right triangle \( …
Choice B
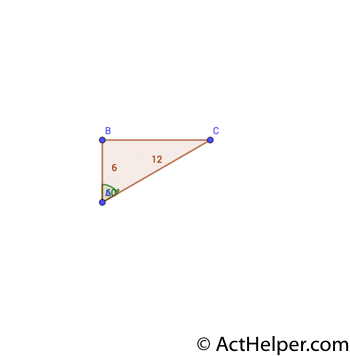
The length of BC can …
Choice F
The volume of the layer …
Choice E
The net profit per batch …
Choice J
The workings are as follows: …
Choice C
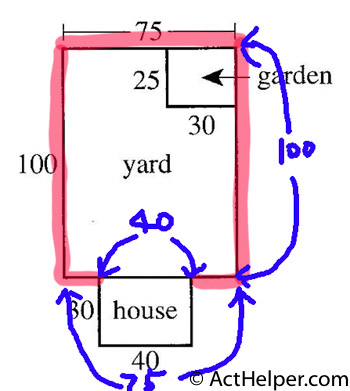
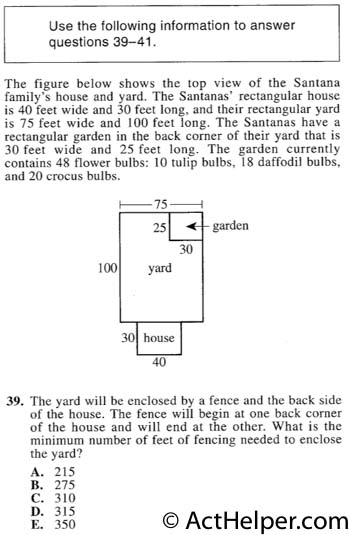
The fence is indicated by …
Choice G
$$ Area \ of\ garden …
Choice B
The number of bulbs in …
Choice J
The amplitude of the function …
Choice B
You can substitute the value …
Choice J
The median would be the …
Choice D
Because the absolute value equation …
Choice F
All we need to do …
Choice B
The circumference ofthe circle = …
Choice F
The question is asking for …
Choice D
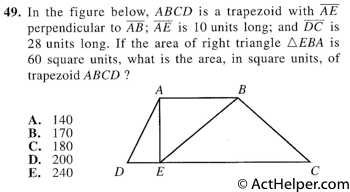
$$ \begin{align} Area \ of\Delta …
Choice F
The decimal repeats in chunks …
Choice C
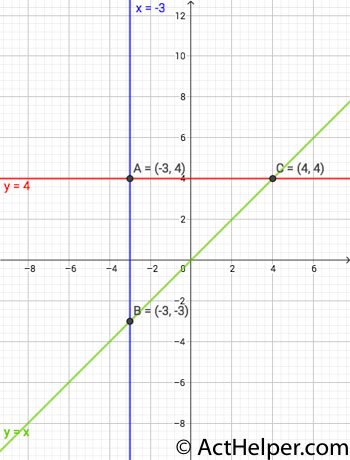
As can be seen in …
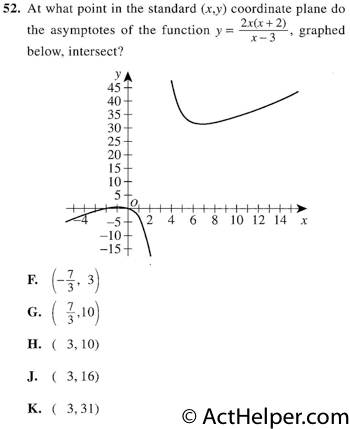
Choice J
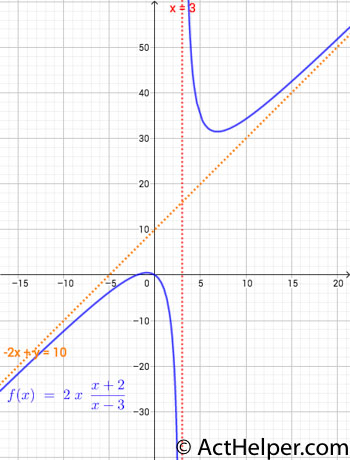
The vertical asymptote \(x=3\) is …
Choice C
The confirmation number will be …
Choice K
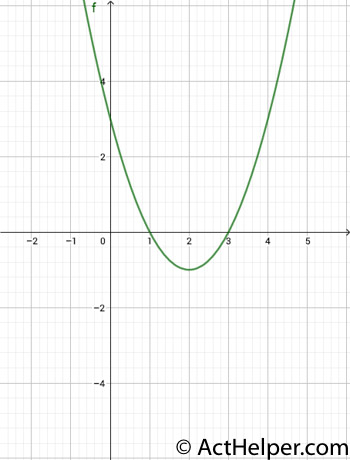
The range of values can …
Choice C
For a matrix A = …
Choice G
The identification code will be in the following format: $$\underline{Digit_1}\ \underline{Letter_1}\ \underline{Letter_2}\ \underline{Letter_3}\ \underline{Letter_4}\ \underline{Digit_2}$$ \(\underline{Digit_1}\) and\(\underline{Digit_2}\) can be any digits from 0-9, while the letters can not be repeated from the 26 English alphabet. Thus the total number of possible codes is: $$10\cdot (26)\cdot (26)\cdot(25)\cdot(24)\cdot(23)\cdot 10$$ of which the number of codes with the fixed letters "MATH" $$ \underline{Digit_1}\ \underline{M}\ \underline{A} \ \underline{T} \ \underline{H}\ \underline{Digit_2} $$ is $$10\cdot 10$$ Therefore, the probability of randomly selecting such a code is: $$\frac{10\cdot 10}{10\cdot (26)\cdot (26)\cdot(25)\cdot(24)\cdot(23)\cdot 10}$$
Choice D
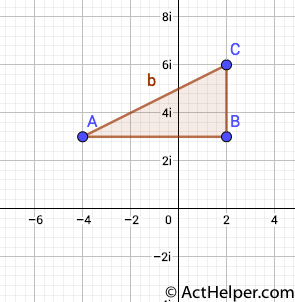
The complex plane is shown below.
With the coordinates A (-4, 3i), C(2, 6i), the distance between A and C is simply $$b=\sqrt{BC^2+AB^2}=\sqrt{3^2+6^2}=\sqrt{45}$$Choice F
To make f(x) as small …
Choice A
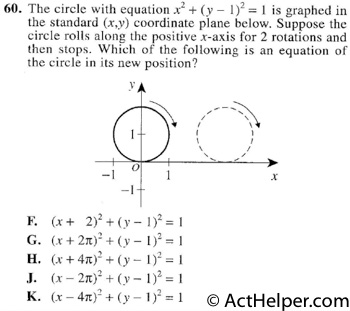
You don’t have to compute …
Choice K
The coordinates of the center …