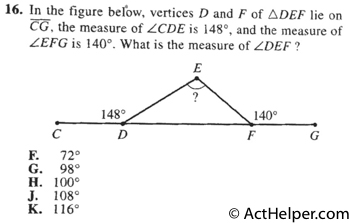
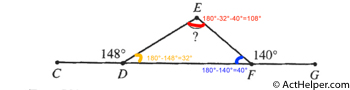
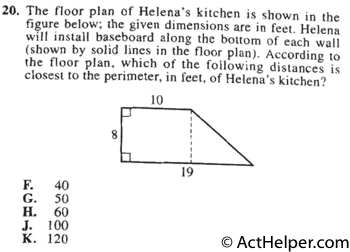
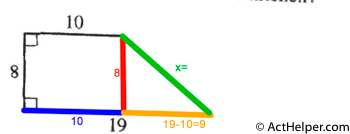
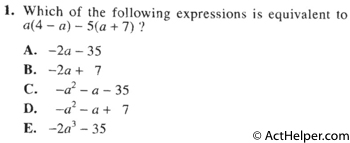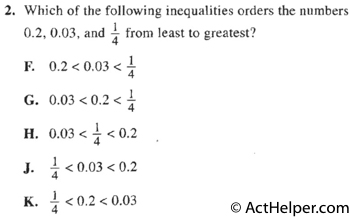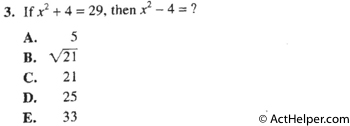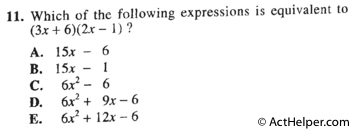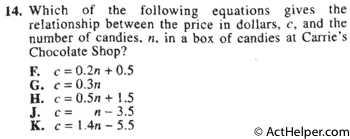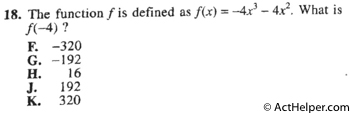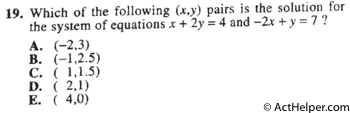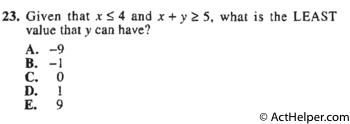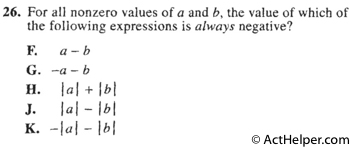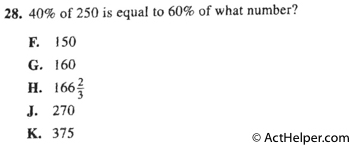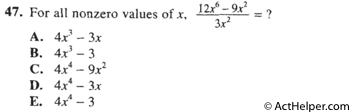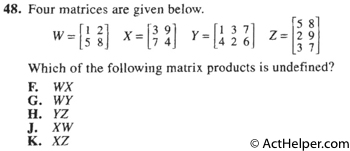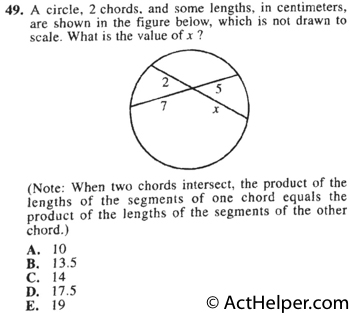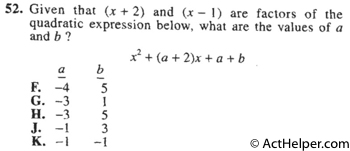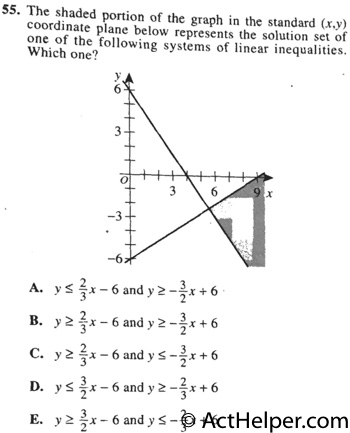Choice G
$$\frac{1}{4}=0.25 \\$$ $$ \Rightarrow 0.03 \leq 0.2 \leq 0.25 \\$$ $$ \Rightarrow 0.03 \leq 0.2 \leq \frac{1}{4}$$
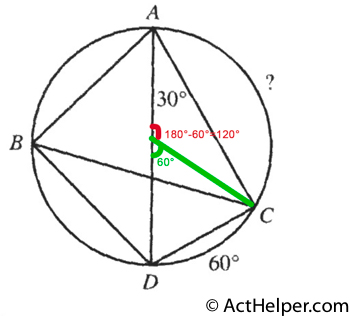
Choice H
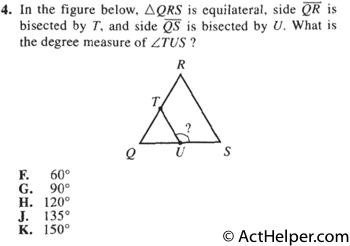
Since T and U bisect QR and QS, respectively, TU//RS. Thus, $$\angle TUQ=\angle S=60° \\$$ $$ \Rightarrow \angle TUS=180°-\angle TUQ=180°-60°=120°$$
Choice K
$$\sqrt{81}=9 \\ $$ $$\sqrt{99}\approx\sqrt{100}=10$$ $$ \\ 9 \leq 9.2371 \leq 10 \\$$ $$ \Rightarrow 81\leq the \ number \leq 99$$
Choice K
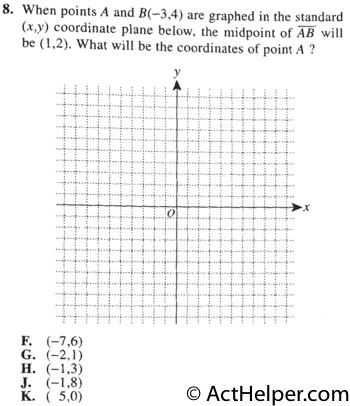
$$\frac{x_{A}+(-3)}{2}=1 \\$$ $$ \Rightarrow x_{A}=5 \\$$ $$ \frac{y_{A}+4}{2}=2 \\$$ $$ \Rightarrow y_{A}=0 $$
Choice J
A box of 25 candies at Tamika's Treat costs $4.25. Thus the money left is $10.00 - $4.25 = $5.75, which is 23 quarters: $$\frac{$5.75}{$0.25}=23$$
Choice F
Only the equation in F fulfils all the given prices and the number of candies given in the table.
Choice C
$$5\times7-4\times6=11$$
Choice H
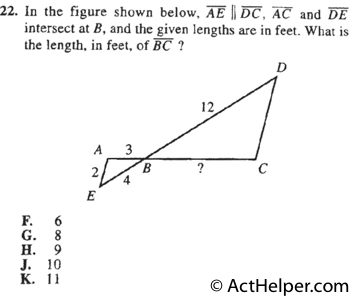
$$\frac{BC}{AB}=\frac{BD}{BE} \\$$ $$ \Rightarrow \frac{BC}{3}=\frac{12}{4} …
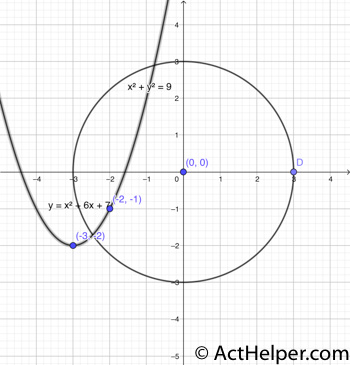
Choice D
When x=4, y can have …
Choice J
Choice D
Let the number of times …
Choice K
Since a and b are …
Choice C
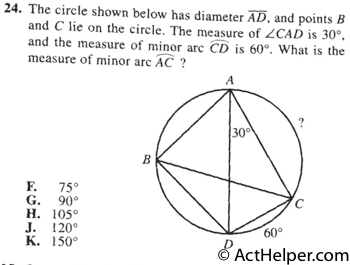
Choice H
$$40\%\times250=60\%x \\$$ $$ \Rightarrow x=166 …
Choice A
$$-2x-6y>2y-4 \\$$ $$ \Rightarrow …
Choice F
$$ \tan\alpha=\frac{\sin\alpha}{\cos\alpha} \\$$ $$ \Rightarrow …
Choice B
$$3k+5k+3k+5k=96 \ cm \\ $$ …
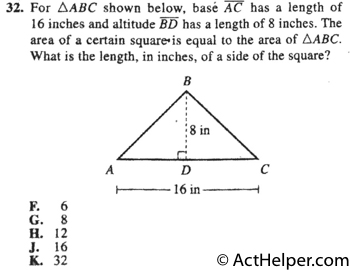
Choice G
$$d^2=\frac{16\times8}{2} \\$$ $$ \Rightarrow d=8 …
Choice B
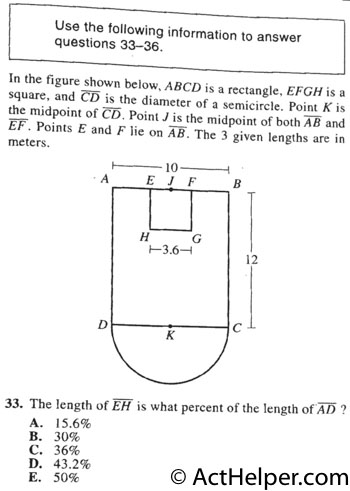
$$\frac{3.6}{12}=30 \%$$
Choice F
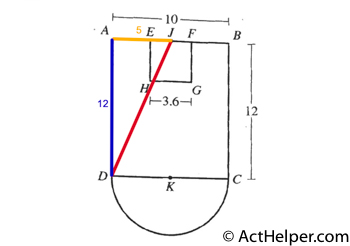
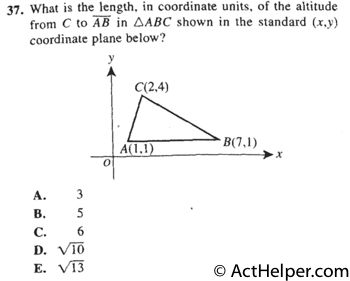
$$JD=\sqrt{5^2+12^2}=13$$
Choice B
$$length \ of arc\ \widehat{CD}=\frac{2\pi …
Choice H
12 - 3.6 = 8.4
Choice A
4 - 1 = 3
Choice J
$$P=\frac{3^ne^{-3}}{n!}=\frac{3^2\times0.05}{2!}\approx0.23$$
Choice B
The amplitude of f(x)=cos(x) is …
Choice H
$$\frac{4}{3}\pi x^3=12 \\ \Rightarrow x=\sqrt[3]{\frac{9}{\pi}}$$
Choice D
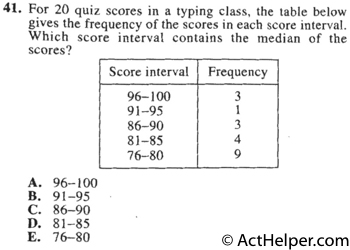
The median will be the …
Choice H
$$\tan40°=\frac{height}{50}\\$$ $$ \Rightarrow height=50\times\tan40°=42$$
Choice B
Sea Horse: $$\frac{255-50-50}{0.25}=620$$ Ocean Blue: …
Choice G
0.05 fits the data best.
Choice A
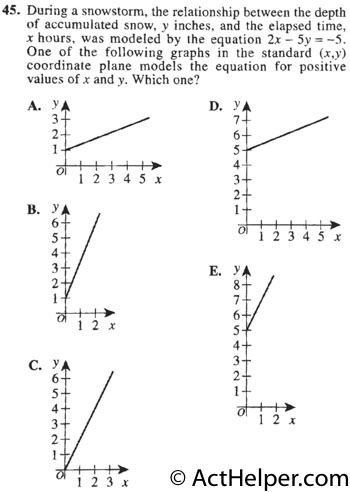
$$2x-5y=-5 \\ $$ $$\Rightarrow 2x+5=5y …
Choice J
$$\frac{x}{2\frac{1}{2}}=\frac{2\frac{1}{4}}{1\frac{1}{2}} \\$$ $$ \Rightarrow x= …
Choice E
$$\frac{12x^6}{3x^2}-\frac{9x^2}{3x^2}=4x^4-3$$
Choice K
XZ is undefined.
https://www.khanacademy.org/math/precalculus/precalc-matrices/multiplying-matrices-by-matrices/v/multiplying-a-matrix-by-a-matrixChoice D
$$2x=5\times7 \\$$ $$ \Rightarrow x=17.5$$
Choice F
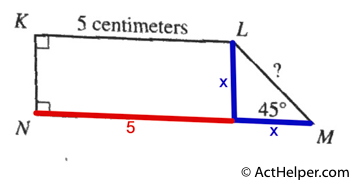
$$\frac{[5+(5+x)]\cdot x}{2}=12 \\$$ $$ \Rightarrow …
Choice B
The square of a number …
Choice K
$$(x-1)(x+2)=x^{2}+x-2$$ $$x^{2}+x-2=x^{2}+(a+2)x+a+b$$ $$\require{cancel}$$ $$\cancel{x^{2}}+x-2=\cancel{x^{2}}+(a+2)x+a+b$$ $$\Rightarrow …
Choice E
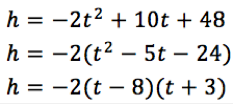
Since the given equation is …
Choice J
The slopes of two lines …
Choice A
The shaded area lies below …
Choice K
$$(\sqrt{3})^{j}=27^{k}$$ $$(3^{\frac{1}{2}})^{j}=(3^{3})^{k}$$ $$\frac{j}{2}=3k$$ $$j=2\times3k$$ $$\frac{j}{k}=6$$ …
Choice A
For an arithmetic sequence, the …
Choice F
$$sin\theta=\frac{1}{4}$$ $$\Rightarrow sin(\frac{1}{4})^{-1}=\theta$$ $$arc\ length=2\pi …
Choice D
The asymptote of a function …
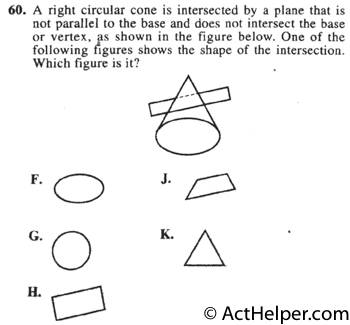
Choice F
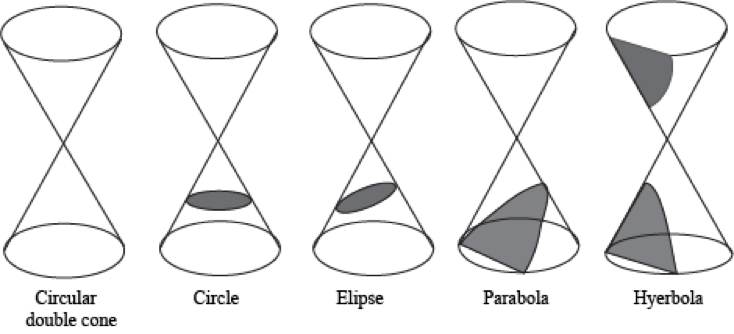
Conic sections are the result …