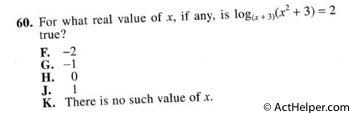Choice D
$$\frac{x}{72}=\frac{1\frac{3}{4}}{24} \\$$
$$ \Rightarrow x=5\frac{1}{4}$$
Choice H
$$\frac{57+61+57+57+58+57}{6}=57.8$$
Choice A
$$120=1.8K-459.67 \\$$
$$ \Rightarrow K\approx 322$$
Choice F
$$-\frac{18}{3}x^{3-1}y^{2-1}=-6x^2y$$
Choice C
$$\sqrt{a}=9 \Rightarrow a=81$$
Choice G
$$\frac{80\times15\%}{5}=2.4$$
Choice B
$$0.000000000087=8.73\times 10^{-11}$$
Choice J
$$\frac{360}{6}=60$$
Choice E
$$\frac{4+45}{9}=\frac{49}{9}$$
Choice G
$$\begin{bmatrix}2\times1+3\times2 & 2\times2+3\times1 \\2\times3-3\times1 & 2\times4-3\times2 \end{bmatrix}=\begin{bmatrix}8 & 7 \\3 & 2 \end{bmatrix}$$
Choice D
The speed of one motorcycle exceeds 4 times the speed of another motor cycle by 24 mph:
4g+24
Choice J
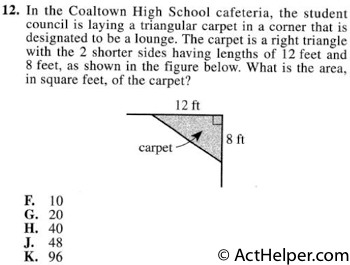
$$Area=\frac{12\times8}{2}=48$$
Choice C
Only the equation in C fulfils all data sets in the table.
Choice H
$$Driving \ time = \frac{1200}{50}=24 \\$$
$$ Unloading \ time = 12 \\$$
$$ \Rightarrow Total \ time=24+12+30=66=24+24+18$$
Choice C
$$x+5y=3 \Rightarrow x=-5y+3$$
Choice H
Thus the other side is also 16; the remaining 2 sides are:
$$\frac{80-16-16}{2}=24$$
Choice D
$$6l+4s=26 \\$$
$$ 2l+4x=14 \\$$
$$ \Rightarrow l=3$$
Choice K
$$2\times6\times5=60$$
Choice C
$$26+2\times5+1.5\times \frac{12}{3}=42$$
Choice E
$$200x=500+20\times30 \\$$
$$ \Rightarrow x=5.5$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
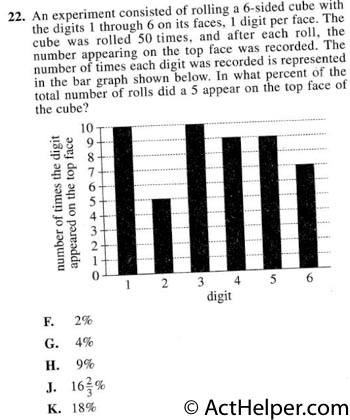
$$\frac{9}{10+5+10+9+9+7}=18\%$$
Choice B
The length of the rectangle is w + 12; the area is $$w\cdot l=140 \\$$
$$ \Rightarrow w\cdot (w+12)=140$$
Choice H
$$\sqrt{(-8-4)^2+(4-9)^2}=\sqrt{169}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice E
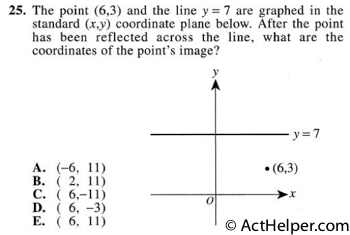
(6,3+(7-3)+(7-3))=(6,11)
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice H
$$Area = \pi r^2=\pi (\frac{6}{2})^2=9 …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice D
$$\frac{99+98+88\times(n-2)}{n}=91 \\$$
$$ \Rightarrow n=7$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice J
Among the choices, only 60 …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice A
$$x^2-x-72=(x-9)(x+8)$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice F
$$Volume=\pi r^2 h=\pi (8^2)(5) \\$$ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
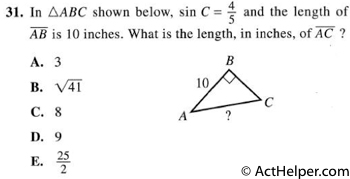
Choice E
$$\sin C= \frac{AB}{AC} \\ $$ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
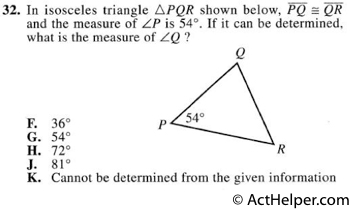
Choice H
$$\angle R= \angle P=54° \\ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice B
g(1) > 0
g(2) > 0
g(3) …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice J
$$b=3n \\$$
$$\Rightarrow \frac{1}{b}+\frac{1}{n}=\frac{1}{3n}+\frac{1}{n}=\frac{...}{3n}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice E
$$g=b+15 \\$$
$$ r=g+24=b+39 \\$$ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
$$(5-2)\times 180°-70°-100°-110°-135°=125°$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
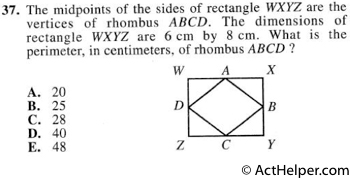
Choice A
$$WD=\frac{6}{2}=3 \\$$
$$ WA=\frac{8}{2}=4 \\$$ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice G
OS=2r
Thus S(0, -2r)
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice B
‘x varies directly with y’ …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice G
$$(|x|-2)(|x|+1)=0 \\$$
$$ \Rightarrow |x|=2 …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice B
The line ST is going …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice H
$$(\frac{1+4}{2},\frac{2+0}{2})=(\frac{5}{2},1)$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice D
$$\tan \angle STR = \frac{SR}{RT}=\frac{2}{3}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice F
SR is the radius which …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice D
A cube has 6 sides. …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
y=-3-5=-8
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice B
$$y=\frac{4}{3}x+\frac{2}{3} \\$$
$$ \Rightarrow slope=\frac{4}{3} …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
K: |x|=x
When x is …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
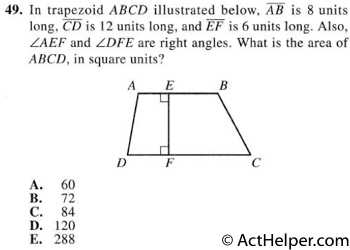
Choice A
$$Area = \frac{AB+CD}{2}\cdot EF=\frac{8+12}{2}\cdot 6=60$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice J
$$x^2={\sqrt{a}}^2=a$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
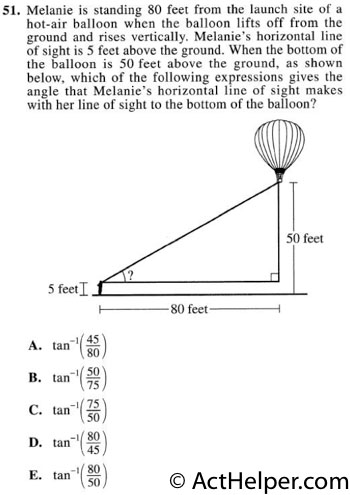
Choice A
$$\tan\alpha=\frac{50-5}{80}=\frac{45}{80}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
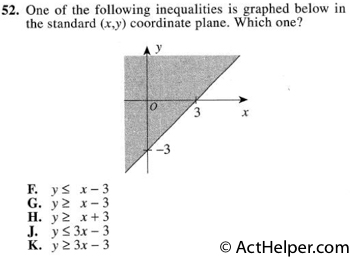
Choice G
Firstly, one need to identify …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice A
$$\frac{3}{6}\cdot\frac{1}{6}=\frac{1}{12}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
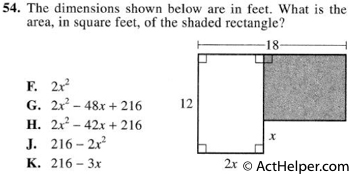
Choice H
$$Area = (18-2x)(12-x)=2x^2-42x_216$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice B
The graph is reflected over …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
$$\frac{x^{24}}{x^6}\cdot x^2=x^{24+2-6}=x^{20}$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice A
$$a\cdot b=-48 \\$$
$$ a+b=0 …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice K
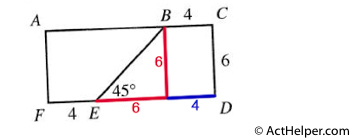
$$Area = 6\times(4+6+4)=84$$
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice A
$$\frac{6}{7}\times \frac{1}{3}\times \frac{1}{100}=\frac{1}{350}$$
Choice A.
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.
Choice G
$$(x+3)^2=x^2+3 \\ $$
$$\Rightarrow x^2+6x+9=x^2+3 …
You are not logged in.
Log In |
Sign Up and pay $59 now to view all explanations.






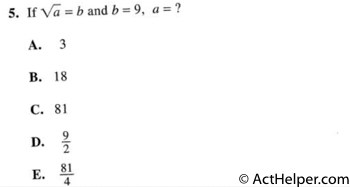

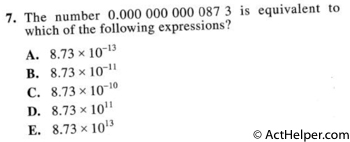


![10. 2[3 24] 2 + 3[-1_2] = ?](/media/questions/72e_math_q10.jpg)