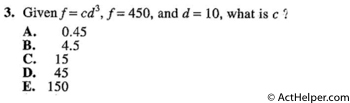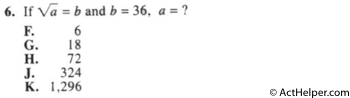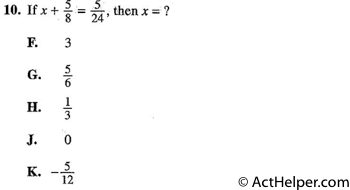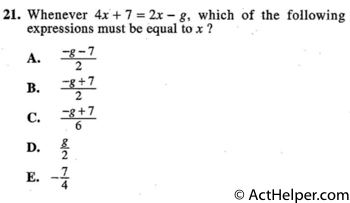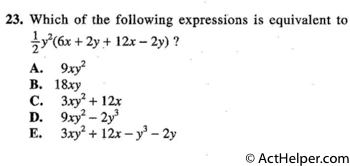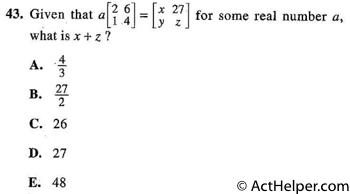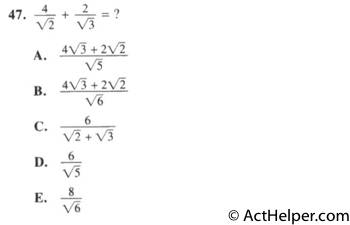Choice C
To calculate the mean of n numbers, take the sum of the n numbers and divide it by n.
$$\frac{$370+$310+$380+$340+$310}{5}=$342$$
Choice H
A discount is a percentage that is subtracted from a number.
For example, a 10% discount of $30 is $3 (10% converted to a decimal is .10 and .10 x 30 is 3).
$12 x 25% = $3
Choice E
In a Geometric Sequence each term is found by multiplying the previous term by a constant.
The constant for the sequence in question is -3. Therefore the sequence is:
1, -3, 9, -27, 81, -243, 729, ...
Choice K
A square root of a number a is a number y such that y^2 = a; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is a. $$\sqrt{a} = 36 \\ ⇒a = 36^2 = 1296$$
Choice K
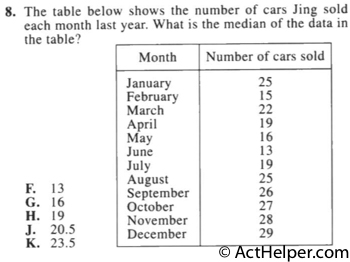
The median of a set of numbers is the middle number in the set (after the numbers have been arranged from least to greatest) -- or, if there are an even number of data, the median is the average of the middle two numbers.
In descending order, the set of numbers is:
13, 15, 16, 19, 19, 22, 25, 25, 26, 27, 28, 29
Median = (22 + 25) / 2 = 23.5
Choice C
A relationship of direct proportionality that, when plotted on a graph, traces a straight line. In linear relationships, any given change in an independent variable will always produce a corresponding change in the dependent variable.
Thus, d = at + k
14 = 0⋅a + k
20 = 1⋅a + k
⇒
k = 14
a = 6
⇒
d = 6t + 14
Choice A
The absolute value of a number is its distance from zero on a number line . For instance, and have the same absolute value (). So, the absolute value of a positive number is just the number itself, and the absolute value of a negative number is its opposite.
|-0.4|= 0.4
|-0.042| = 0.042
|-0.0048| = 0.0048
|0.04| = 0.04
|0.047| = 0.047
Choice G
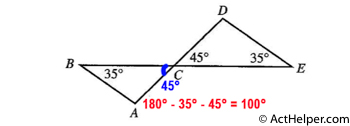
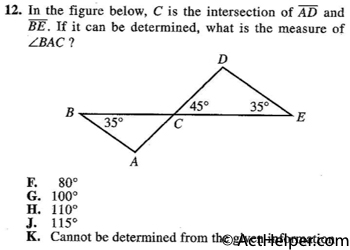
The sum of measures of three angles of any triangle is invariably equal to 180°.
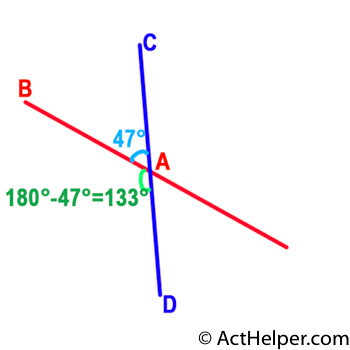
Vertical Angles are angles opposite each other when two lines cross. They are always equal.
∠A = 180° - 35° - 45° = 100°
Choice B
Let the number of large figurines be L;
Let the number of small figurines be S;
L + S = 70
12⋅L = 8⋅S
L = 28, S= 42
Choice C
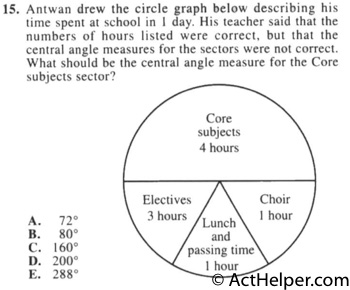
A circle has a total of 360 degrees all the way around the center.
So if that central angle determining a sector has an angle measure of 60 degrees, then the sector takes up 60/360 or 1/6, of the degrees all the way around.
$$\frac{4}{4+1+1+3}\times 360°= 160°$$
Choice K
To find the area of a rectangle, multiply the length by the width. The formula is: A = L * W where A is the area, L is the length, W is the width, and * means multiply.
The perimeter of a rectangle is equal to the sum of all the sides. However, since a rectangle's opposite sides are congruent, we only need to know the length and width.
L × W = 32
L = 2W
⇒ W = 4, L = 8
⇒ Perimeter = (4 + 8) × 2 = 24
Choice C
Given the final speed, vf (which is 220 fps), and the initial speed, vi (which is 88 fps), and you know the time needed (3 seconds), you can find the acceleration, a. Because vf – vi = a⋅t
vf – vi = a⋅t
⇒ 220 - 88 = 3a
⇒ a = 44
Choice J
Scientific notation is a way of writing very large or very small numbers. A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10. For example, 650,000,000 can be written in scientific notation as 6.5 ✕ 108
670,000,000 + 700,000,000 = 1,370,000,000 = 1.37 ✕ 109
Choice H
| Rule name | Rule | Example |
|---|---|---|
| Product rules | a n ⋅ a m = a n+m | 23 ⋅ 24 = 23+4 = 128 |
| a n ⋅ b n = (a ⋅ b) n | 32 ⋅ 42 = (3⋅4)2 = 144 | |
| Quotient rules | a n / a m = a n–m | 25 / 23 = 25-3 = 4 |
| a n / b n = (a / b) n | 43 / 23 = (4/2)3 = 8 | |
| Power rules | (bn)m = bn⋅m | (23)2 = 23⋅2 = 64 |
| bnm = b(nm) | 232 = 2(32)= 512 | |
| m√(bn) = b n/m | 2√(26) = 26/2 = 8 | |
| b1/n = n√b | 81/3 = 3√8 = 2 | |
| Negative exponents | b-n = 1 / bn | 2-3 = 1/23 = 0.125 |
| Zero rules | b0 = 1 | 50 = 1 |
| 0n = 0 , for n>0 | 05 = 0 | |
| One rules | b1 = b | 51 = 5 |
| 1n = 1 | 15 = 1 | |
| Minus one rule | (-1)n = -1 , n odd v (-1)n = 1 , n even |
(-1)5 = -1 |
| Derivative rule | (xn)‘ = n⋅x n-1 | (x3)‘ = 3⋅x3-1 |
| Integral rule | ∫ xndx = xn+1/(n+1)+C | ∫ x2dx = x2+1/(2+1)+C |
$$\Rightarrow \frac{(3x)^2}{x^5}=\frac{9x^2}{x^5}=\frac{9}{x^{5-2}}=\frac{9}{x^{3}}$$
Choice A
⇒ 4x - 2x = …
Choice F
When parallel lines get crossed …
Choice A
$$\require{cancel} \frac{1}{2}\cdot y^{2}(6x+2y+12x-2y)$$ $$\Rightarrow \frac{1}{2}\cdot …
Choice F
Plugging in the numbers in …
Choice D
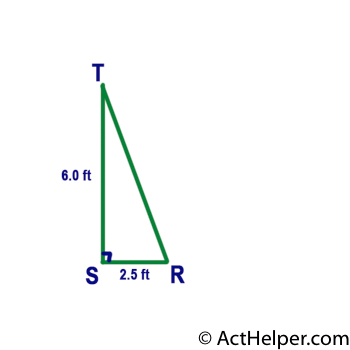
The Pythagorean theorem states that, …
Choice H
The phrase "At least" means …
Choice B
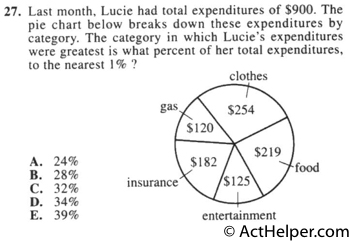
Among the categories of expenditures, …
Choice G
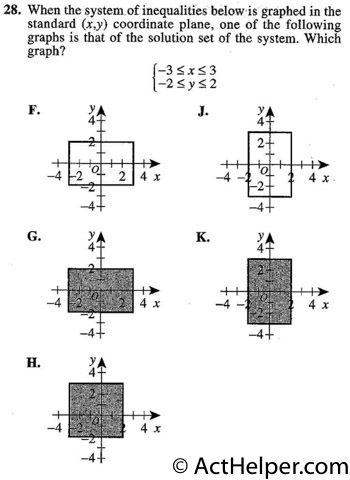
To graph a linear inequality, …
Choice B
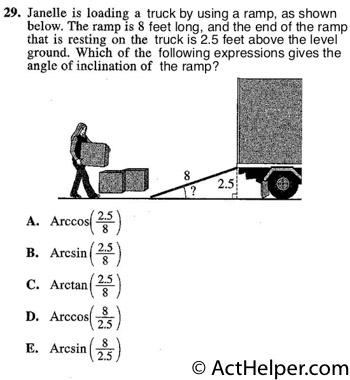
To obtain an angle from …
Choice K
An Isosceles Right Triangle is …
Choice C
As we can see from …
Choice G
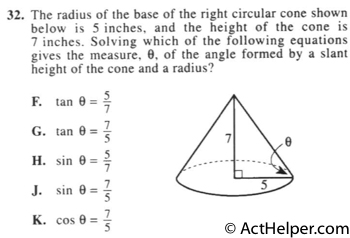
To obtain an angle from …
Choice D
The formula can be rearranged …
Choice J
The probability of selecting an …
Choice B
The perimeter of a rectangle …
Choice H
Plugging the data in the …
Choice B
It is given in the …
Choice H
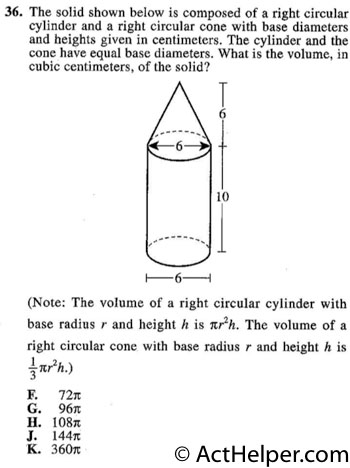
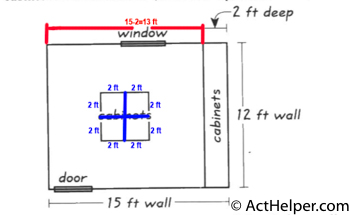As we can see from …
Choice D
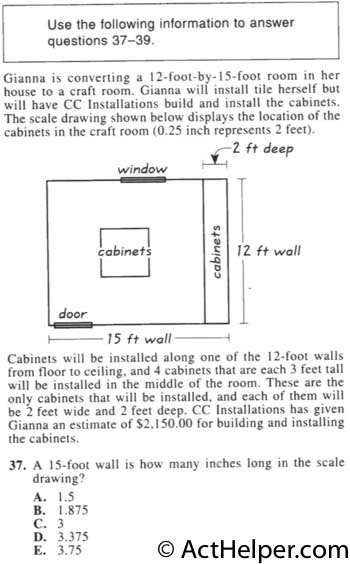
The cabinet charge out of …
Choice G
Given any two points on …
Choice A
The rule for a reflection …
Choice K
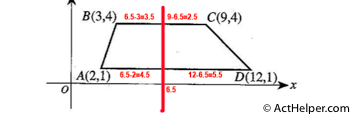
A line perpendicular to the …
Choice D
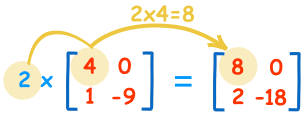
To multiply a matrix by …
Choice G
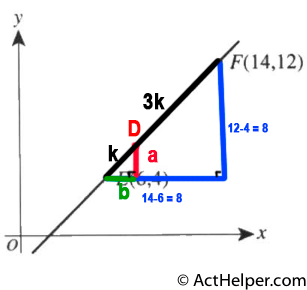
With the supplemented lines, we …
Choice E
The perimeter of a triangle …
Choice K
To calculate the mean of …
Choice B
To add fractions there are …
Choice J
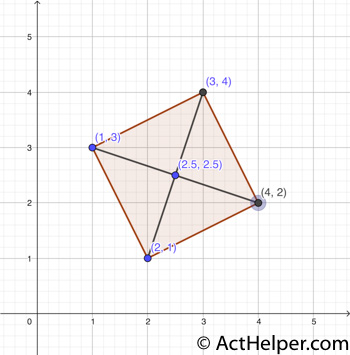
The center of rectangle is …
Choice A
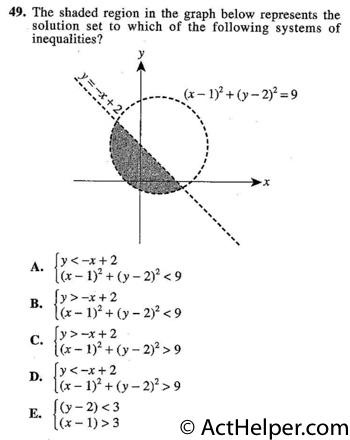
To graph inequalities, first, graph …
Choice F
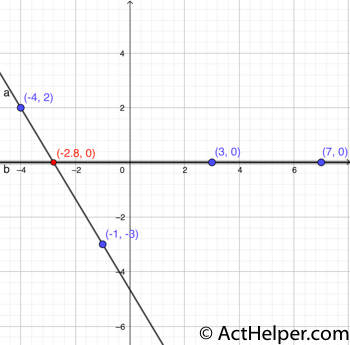
It should be noted that …
Choice D
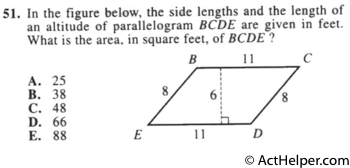
The area of a parallelogram …
Choice K
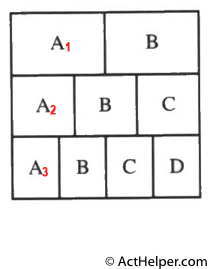
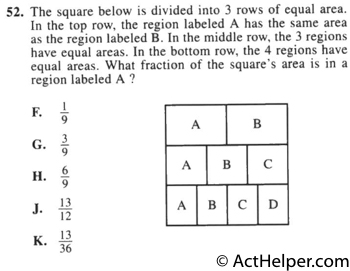
$$A_{1}=\frac{1}{2}\cdot\frac{1}{3}Area_{Square} \\$$ $$ A_{2}=\frac{1}{3}\cdot\frac{1}{3}Area_{Square} \\$$ …
Choice A
Factoring 9x2+12x+4=0, we …
Choice H
$$40\% \times 60 + a\times40=36\%\times100 …
Choice E
The square root must be …
Choice F
It can be observed that …
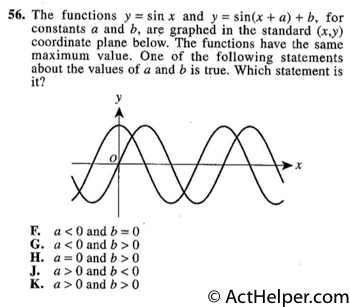
Choice E
The absolute value of a …
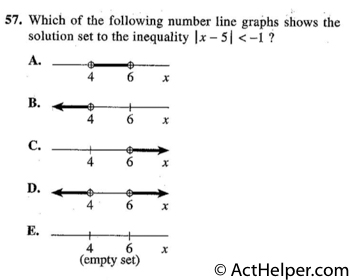
Choice J
The smallest angle must be …
Choice D
To reduce a fraction to …
Choice J
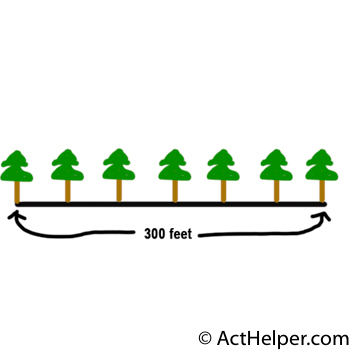
As we can see from …