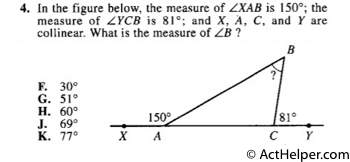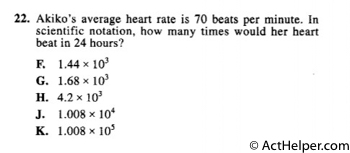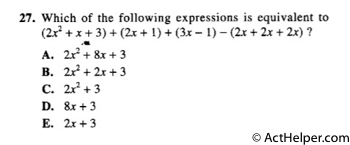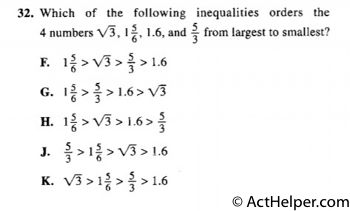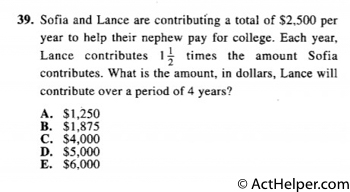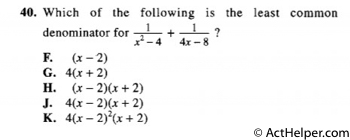Choice B
$$\angle BCA=180°-81°=99°$$ $$\angle BAC=180°-150°=30°$$ $$\angle B=180°-99°-30°=51°$$
Choice K
$$(-3)^{2}(2)^{3}-(-3)(2)^{2}+(-3)$$ $$=9\times8+3\times4-3$$ $$=72+12-3$$ $$=81$$
Choice C
$$2\times60=120$$ $$120\div5=24$$ $$24\times11=264$$ $$\because 1\ ft= 12\ inches$$ $$264\div12=22$$
Choice H
$$\frac{1}{2}\times24=12$$ $$\frac{2}{3}\times24=16$$ $$\frac{5}{6}\times24\times2=20\times2=40$$ $$12+16+40=68$$
Choice A
Any point that is 3 units from (6, 4) could be an adjacent vertex to the vertex at (6, 4).
The most obvious points that are 3 units from (6, 4) will share either the x or the y coordinate with (6, 4) and have the other coordinate 3 units greater than or less than that of (6, 4).
A is the correct answer
Choice K
$$\frac{1}{8}+\frac{3}{4}=\frac{7}{8}$$ $$\frac{7}{8}\times2=\frac{7}{4}=1\frac{3}{4}$$
Choice D
$$(6+15+20+30)\div4$$ $$=71\div4$$ $$=17\frac{3}{4}$$
Choice F
$$33\times30000=990000$$ $$990000\times0.06=59400$$ $$30\times30000=900000$$ $$900000\times0.07=63000$$ $$63000-59400=3600$$
Choice A
$$=\frac{1}{5}\times\frac{a^{5}}{a^{2}}\times\frac{b^{3}}{b^{7}}\times\frac{c^{4}}{c}$$ $$=\frac{1}{5}\times a^{3}\times \frac{1}{b^{4}}\times c^{3}$$ $$=\frac{a^{3}c^{3}}{5b^{4}}$$
Choice K
$$24\ hrs=24\times60=1440\ mins$$ $$70\times1440=100800=1.008\times10^{5}$$
Choice D
$$5x+6x+9x=20x=100$$ $$x=5$$ $$9x=9\times5=45$$
Choice H
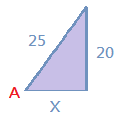
$$25^{2}=20^{2}+x^{2}$$ $$x=15$$ $$\tan A=\frac{20}{15}$$
Choice E
Using the Pythagorean Theorem until …
$$2x+3y-1=0$$ $$\because y=mx+b$$ $$\Rightarrow 3y=-2x+1$$ …
Choice C
$$=(2x^{2})+(x+2x+3x-2x-2x-2x)+(3+1-1)$$ $$=2x^{2}+3$$
Choice K
$$1 feet = 12 inches$$ …
Choice C
$$C=3.5A+120$$ $$C=3.5(270)+120$$ $$=1065$$
Choice J
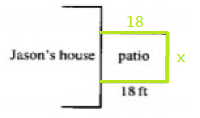
$$270=18\times x$$ $$x=15$$ $$18+18+15=51$$
Choice C
$$\sin\theta=\frac{10000}{8\times5280}$$ $$\theta=\arcsin\frac{10000}{8\times5280}$$
Choice F
$$\sqrt{3}\approx1.732$$ $$1\frac{5}{6}=1.83$$ $$\frac{5}{3}=1.67$$
Therefore, F …
Choice E
$$\frac{-2}{1}=-2$$ $$\frac{4}{-2}=-2$$ $$\Rightarrow 1,-2,4,-8,16,-32,64$$
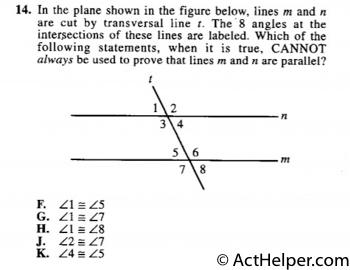
Choice F
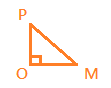
(F) could be true because …
Choice C
$$\frac{\triangle ABC}{\triangle DEF}$$ $$=\frac{2}{3}$$ $$=\frac{20}{x}$$ …
Choice G
(G) 40% of net sales …
Choice B
$$\tan35°=\frac{?}{450}$$ $$\Rightarrow ?=450\tan35°$$
Choice G
$$\frac{5+3x}{2}-3\gt0$$ $$\Rightarrow \frac{5+3x}{2}\gt 3$$ $$\Rightarrow …
Choice E
$$\frac{1.5}{1.5+1}=\frac{1.5}{2.5}$$ $$\frac{1.5}{2.5}=\frac{x}{2500}$$ $$\Rightarrow x = …
Choice J
$$x^{2}-4=x^{2}-2^{2}=(x+2)\times(x-2)$$ $$4x-8=4\times(x-2)$$ $$\Rightarrow\frac{1}{(x+2)(x-2)}+\frac{1}{4\times(x-2)}$$ $$\Rightarrow (x+2)\times(x-2)\times4$$
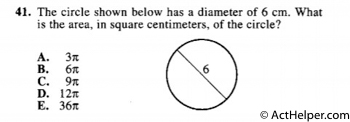
Choice C
$$\pi r^{2}=\pi\times3^{2}=9\pi$$
Choice F
$$Slope=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$ $$=\frac{-2-(-5)}{10-(-2)}=\frac{1}{4}$$
Plug this slope …
Choice E
The 53 people who used …
Choice H
$$3\times7=21$$ $$21\times4=84$$
Choice A
$$\frac{1}{4}\times-4=-1$$
Choice J
The helicopter is 2 + …
Choice D
2 is the only even …
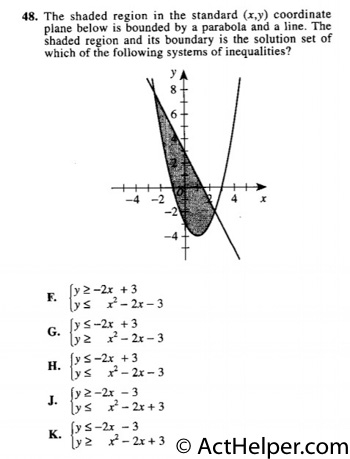
Choice G
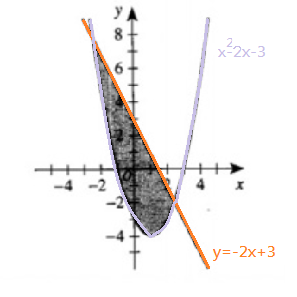
(G) The shaded region involves …
Choice A
$$x+y=-a---(1)$$ $$x-y=b---(2)$$ $$(1)-(2)$$ $$\Rightarrow (x+y)-(x-y)=-a-b$$ …
Choice G
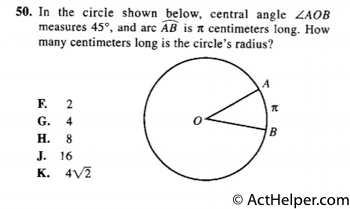
$$2\pi r\times\frac{45}{360}$$ $$=2\pi r\times\times\frac{1}{8}$$ $$=\frac{1}{4}\pi …
Choice A
$$3a=b---(1)$$ $$8a-2=b---(2)$$ $$(2)-(1)$$ $$5a-2=0$$ $$a=\frac{2}{5}$$
Choice G
$$x^{2}+2ax+a^{2}$$ $$\Rightarrow 2a=-6$$ $$\Rightarrow a=-3$$
Choice D
A complete revolution is equivalent …
Choice K
The denominator of any fraction …
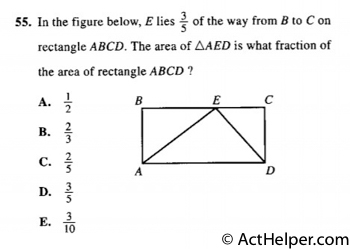
Choice A
The area of a rectangle …
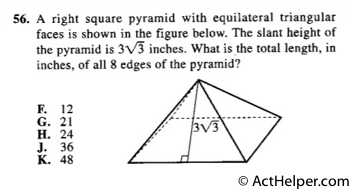
Choice K
These triangles are equilateral.
Each …
Choice D
$$I.$$ $$ -3-(-7)=4,\ -3-(0)=3$$ $$\sqrt{4^{2}+3^{2}}=5$$ …
Choice J
There are 25 even numbers …
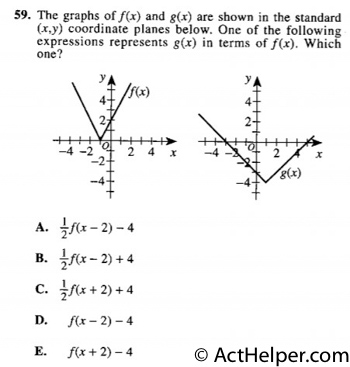
Choice A
f(x)– 4 represents a shift …
Choice K
Those statements are equivalent:
If …