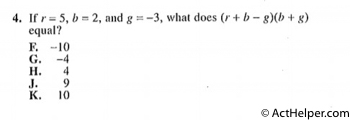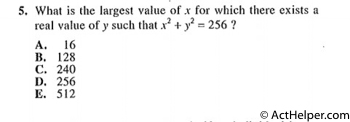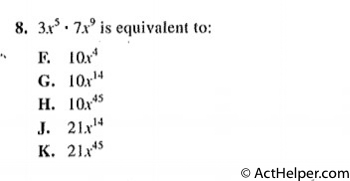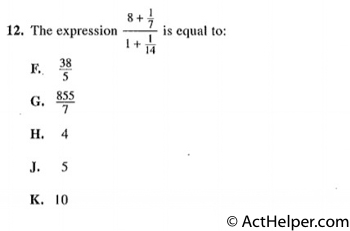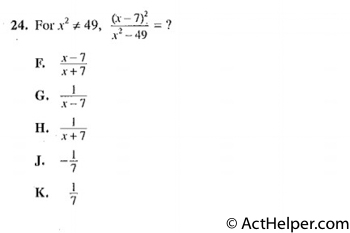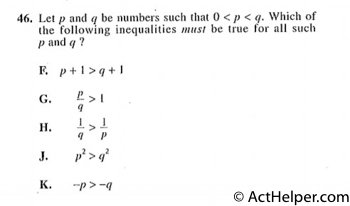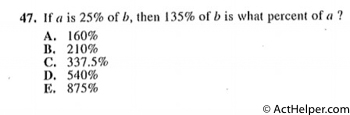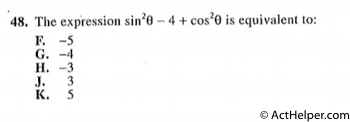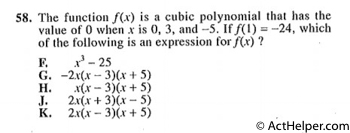Choice A
To maximize the value of x, you must minimize the value of
$$y^{2}$$ $$y^{2}=0,\ x^{2}=256$$ $$x=\pm\sqrt{256}=\pm16$$The positive 16 is the answer.
Choice C
$$N(4)=\frac{1200\times4^{2}+10}{4^{2}+1}$$ $$=\frac{1200\times16+10}{16+1}$$ $$=\frac{19200}{17}$$ $$\approx 1130$$
Choice G
$$35=5\times7$$ $$56=2^{3}\times7$$ $$16=2^{4}$$ $$\Rightarrow2^{4}\times5\times7=16\times5\times7=560$$
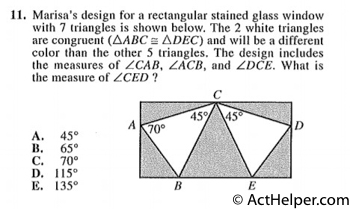
Choice B
Because triangles ABC and DEC are congruent,
$$\angle CAB=\angle CDE$$ $$\angle CDE= 180° – 45° – 70° = 65°$$Choice F
$$=\frac{\frac{57}{7}}{\frac{15}{14}}$$ $$=\frac{57}{7}\times\frac{14}{15}$$ $$=\frac{114}{15}$$ $$=\frac{38}{5}$$
Choice D
$$x + y = 15 ---(1)$$ $$x – y = 9---(2)$$ $$(1)+(2)$$ $$2x=24$$ $$x=12$$ $$y=3$$ $$xy=12(3)=36$$
Choice J
1. Draw A as a point on a circle.
2. Draw B 6 units counterclockwise from A.
3. Draw C 2 units clockwise from point A, between A and B in the clockwise direction.
4. Draw D 9 units clockwise from A, between C and B in the clockwise direction.
Now your points are in the correct order, A, C, B, D in the clockwise direction.
Choice K
$$ Slope-intercept (y = mx + b) form$$ $$ 6x – 2 = y \Rightarrow y = 6x – 2$$
Choice K
$$Slope=\frac{(y2 – y1)}{(x2 – x1)}$$ $$=\frac{10-8}{-2-3}$$ $$=\frac{2}{-5}$$
Choice E
$$a + a + b …
Choice H
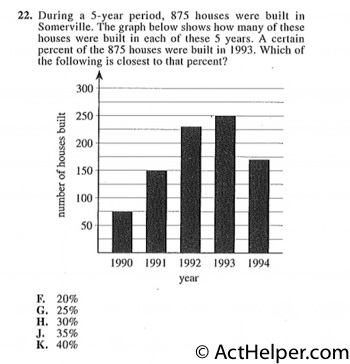
$$\frac{250}{875}$$ $$=0.286 $$
Choice B
$$37-13=24$$ $$24=3\times8$$ $$13,16,19,22,25,28,31,34,37$$
The question …
Choice F
$$x^{2}\neq49\Rightarrow x\neq\pm7$$ $$x^{2}-49=(x+7)(x-7)$$ $$\Rightarrow\frac{(x-7)(x-7)}{(x+7)(x-7)}$$ $$=\frac{(x-7)}{(x+7)}$$
Choice C
$$12:8=15:x$$ $$8\times15=12x$$ $$x=10$$
Choice H
When x -2, (x + …
Choice B
$$z + 2(z + 2) …
Choice G
B is 10 blocks east …
Choice E
$$b=6c \Rightarrow c=\frac{1}{6}b$$ $$a=2c=2(\frac{1}{6}b)=\frac{1}{3}b$$
Choice J
$$\frac{5}{9}(59-32)=\frac{5}{9}\times27=15$$ $$\frac{5}{9}(68-32)=\frac{5}{9}\times36=20$$ $$\Rightarrow 15° \leq …
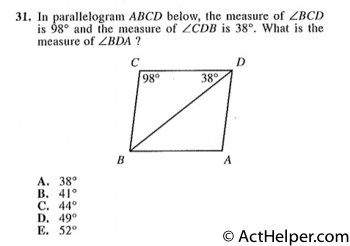
Choice C
By parallel line properties,
$$\angle …Choice J

$$6\times6\times5=180$$
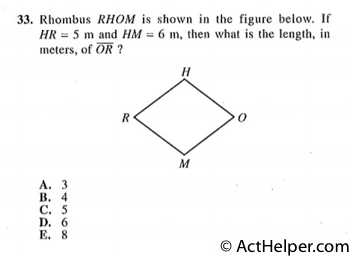
Choice E
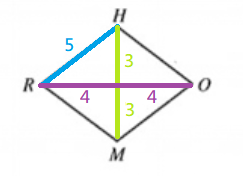
The triangle is a 3-4-5 …
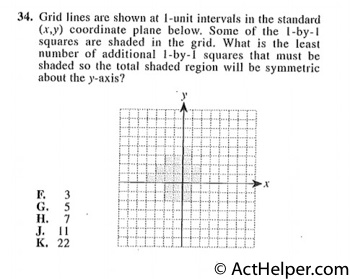
Choice H
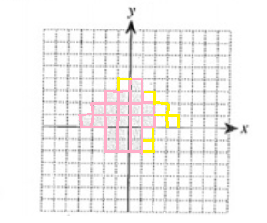
Shade any square whose reflection …
Choice C
$$4x(x)=80$$ $$\Rightarrow 4x^{2}=80$$ $$\Rightarrow x=\sqrt{20}$$ …
Choice K
The volume of this rectangular …
Choice B
$$t = 10f – 20$$ …
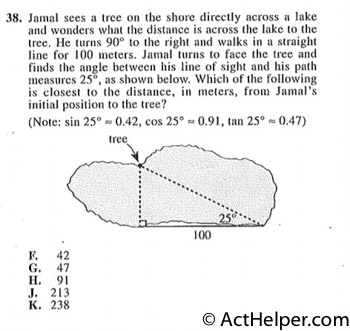
Choice G
$$Tangent=\frac{opposite}{adjacent}$$ $$\tan25°=\frac{x}{100}$$ $$x=100\tan25°=100\times0.47=47$$
Choice E
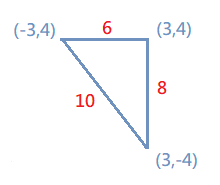
3-4-5 triangle (6-8-10)
Choice J
$$4^{3}=64$$ $$4\times3=12$$ $$12^{3}=1728$$
The volume …
Choice E
$$(x-h)^{2}+(y-k)^{2}=r^{2}$$
Based on this equation, …
Choice J
The perimeter of a rectangle …
Choice A
There are 2 possible vertical …
Choice F
The current area of the …
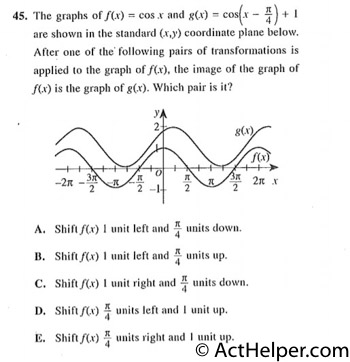
Choice E
Compared to y = cos …
Choice K
$$0\lt p\lt q$$
(F)\ 0\lt …
Choice D
$$a=b\times0.25$$ $$\frac{b\times1.35}{b\times0.25}=\frac{1.35}{0.25}=5.4$$
Choice H
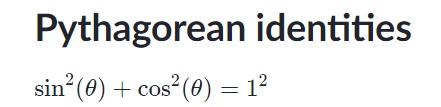
$$\sin^{2}\theta+\cos^{2}\theta-4$$ $$=1-4$$ $$=-3$$
Choice E
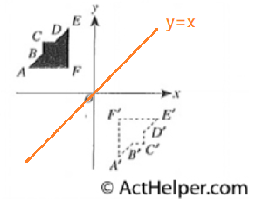
Therefore, the line of reflection …
Choice H
$$\frac{x}{144°}=\frac{60}{360°}$$ $$x=144\times\frac{60}{360}=24$$
Choice B
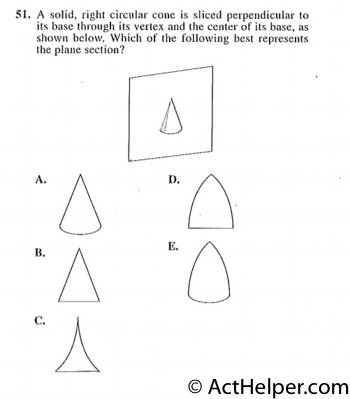
The plane section of such …
Choice F
$$\log x=y \Rightarrow a^{y}=x$$ $$b^{4}=81$$ …
Choice D
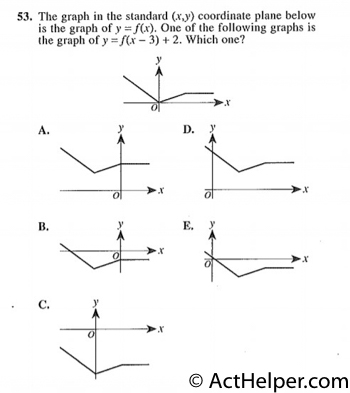
f(x + a) + b …
Choice F
Based on parallel line properties, …
Choice D
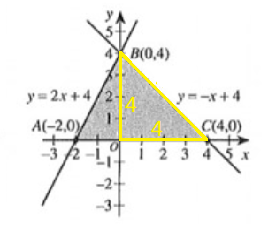
To maximize the value of P(x,y), you must maximize the value of 4x + 3y.
At point B, P(x,y) = 4 • 0 + 3 • 4 = 12.
At point C, P(x,y) =4 • 4 + 3 • 0 = 16.
The value of P(x,y) is higher at point C then at point B and points B and C are connected by a straight line delineating an edge of the shaded region, no other points along this line or anywhere else in the shaded region can have a higher value than point C.
Choice F
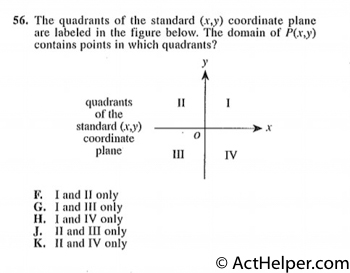
(F) Look at the graph of P(x,y) above question 55 and compare it to the graph in 56 that labels the quadrants. P(x,y) contains points in quadrants I and II only.
Choice A
Tangent is defined as opposite/adjacent. …
Choice K
If f(x)=0 when x=3, (x …
Choice C
$$\frac{5}{1000000}=5\cdot 10^{-6}$$
Choice F
$$(a^{2}-b^{2})=(a+b)(a-b)$$ $$(a – b)\gt (a …