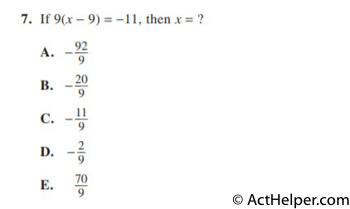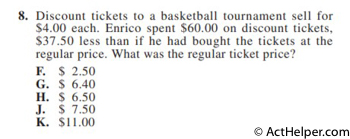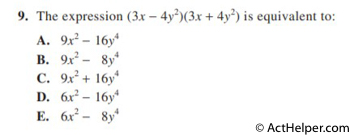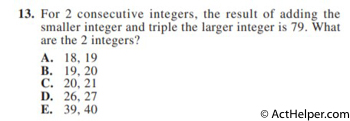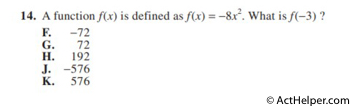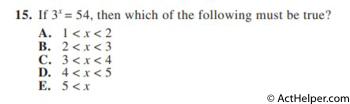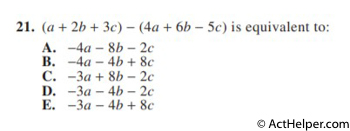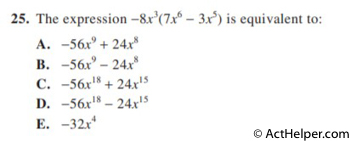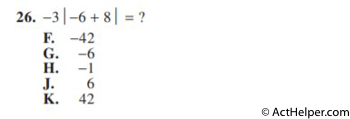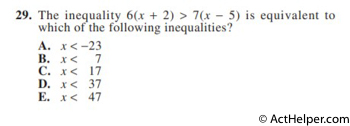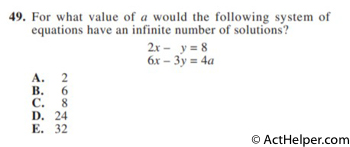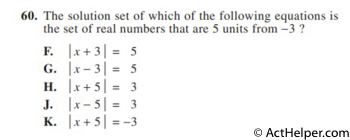Choice E
$$1st\ machine:60\times8=480$$ $$2nd\ machine:80\times6=480$$ $$\Rightarrow 480+480=960$$
Choice E
$$9(x-9)=-11$$ $$\Rightarrow 9x-81=-11$$ $$\Rightarrow 9x=70$$ $$\Rightarrow x=\frac{70}{9}$$
Choice A
$$=(3x)(3x+4y^{2})-(4y^{2})(3x+4y^{2})$$ $$=(9x^{2})+(12xy^{2})-(12xy^{2})-(16y^{4})$$ $$=9x^{2}-(16y^{4})$$
Choice B
Consecutive integers can be represented as (n, n + 1).
$$n+ 3 n + 1 = 79$$ $$4n + 3 = 79$$ $$n = 19$$Choice C
$$3^{x}=54$$ $$3^{3}=27$$ $$3^{4}=81$$ $$\Rightarrow 3^{3}\lt 3^{x}\lt 3^{4}$$ $$\Rightarrow 3\lt {x}\lt {4}$$
Choice J
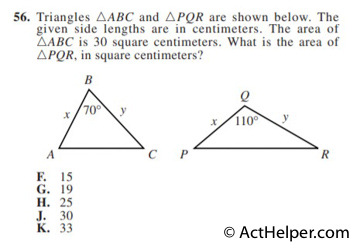
$$70=7\times10$$ $$60=6\times10$$ $$50=5\times10$$ $$7\times6\times5\times10=2100$$
Choice J
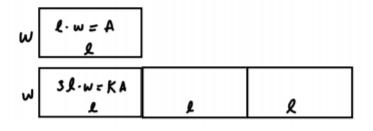
$$Smaller\ Rectangle=l\cdot w=A$$ $$Larger\ Rectangle=3l \cdot w =kA$$ $$k=3$$
Choice E
$$=(a-4a)+(2b-6b)+(3c+5c)$$ $$=-3a-4b+8c$$
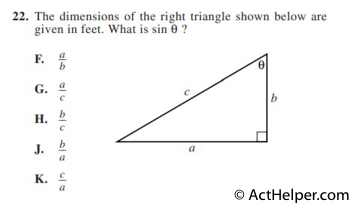
Choice G
$$\sin\theta=\frac{Opp}{Hyp}$$ $$\sin\theta=\frac{a}{c}$$
Choice B
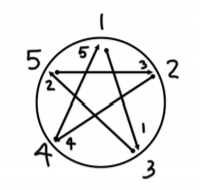
Let five players be A, …
Choice H
$$y=0.12x+3000$$ $$\Rightarrow m=0.12$$ $$0.12+0.1=0.22$$
Choice A
$$=-8(7)(x^{3+6})+(-8)(-3)(x^{3+5})$$ $$=-56x^{9}+24x^{8}$$
Choice G
$$=-3\mid2\mid$$ $$=-3(2)$$ $$=-6$$
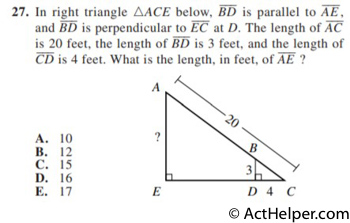
Choice B
$$3-4-5\ triangle \Rightarrow \overline{BC}=5$$ $$\overline{AC}:\overline{BC}=20:5=4:1$$ …
Choice H
“Constant rate.” - This is …
Choice E
$$\Rightarrow 6x+12 \gt 7x-35$$ $$\Rightarrow …
Choice K
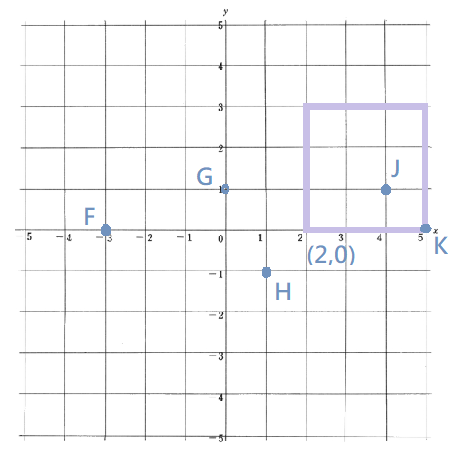
Only K is 3 units …
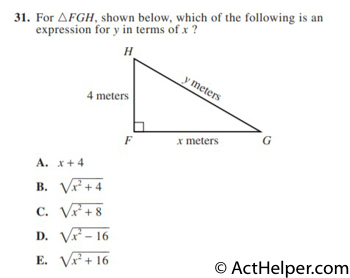
Choice E
$$A^{2}+B^{2}=C^{2}$$ $$y^{2}=x^{2}+4^{2}$$ $$y=\sqrt{x^{2}+16}$$
Choice G
$$\frac{12+x}{32+x}=\frac{3}{5}$$ $$5(12+x)=3(32+x)$$ $$60+5x=96+3x$$ $$2x=36$$ $$x=18$$
Choice D
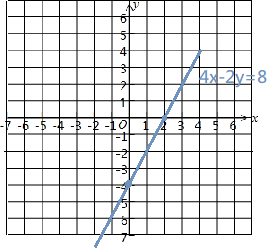
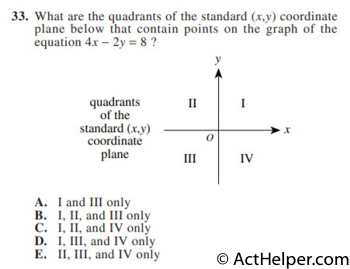
$$4x-2y=8$$ $$\Rightarrow 2x-y=4$$ $$(x,y)\Rightarrow (0,-4),(2,0)$$
Choice F
$$2a=-5(1)^{2}+9$$ $$2a=-5+9=4$$ $$a=2$$
Choice D
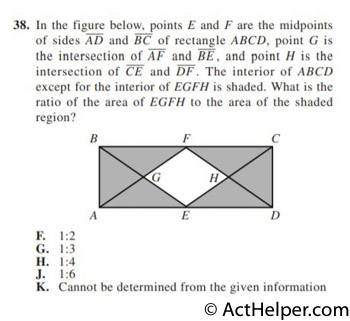
$$\frac{1}{2}S+\frac{1}{3}S+xS=S$$ $$\Rightarrow x=\frac{1}{6}$$ $$\frac{1}{2}:\frac{1}{3}:\frac{1}{6}=3:2:1$$
Choice F
The equation of a circle …
Choice B
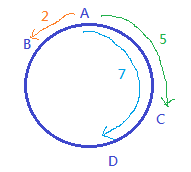
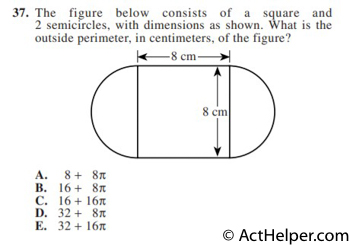
2 semicircles make one circle, …
Choice G
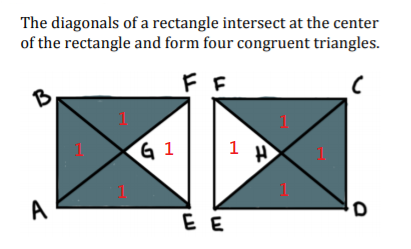
$$\triangle EGF=\triangle EHF=\triangle BAG=\triangle CDH$$
Choice C
$$The\ midpoint$$ $$=(\frac{(-4+14)}{2},\frac{,(-2+2)}{2})$$ $$=(5,0)$$
Choice G
$$Area\ of\ one\ face\ of\ …
Choice B
$$ay+bx=x$$ $$ay$$ $$\Rightarrow y=-\frac{b}{a}+\frac{c}{a},\ m=-\frac{b}{a}$$ …
Choice F
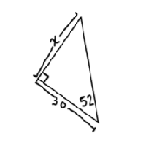
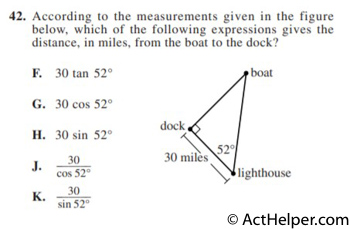
From the angle of 52, …
Choice D
Odd- in age: not in …
Choice H
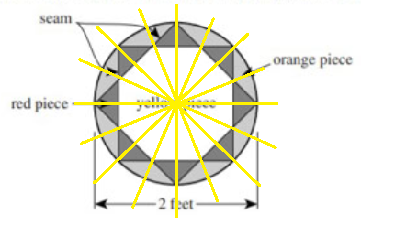
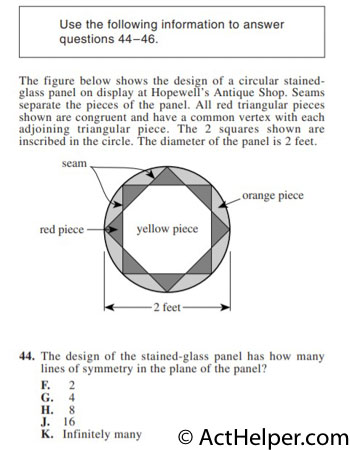
“Lines of symmetry” are lines …
Choice A
$$Diameter=2, so radius=1$$ $$Area=\pi r …
Choice J
Diameter=2, 75% longer
$$2\times1.75=3.5$$Choice C
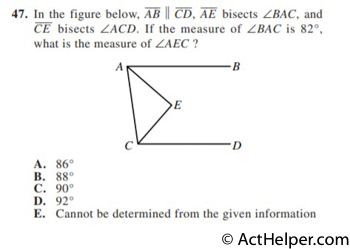
$$\angle BAC=82°$$ $$\angle ACD=180°-82°=98°$$ $$\angle …
Choice H
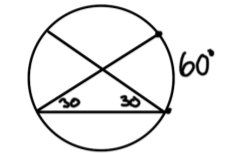
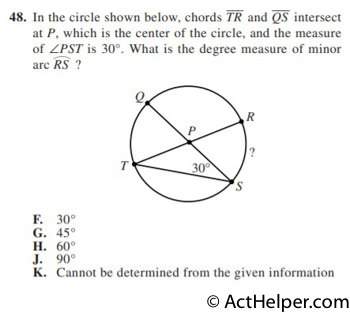
Arc angle is twice the …
Choice B
Infinite solutions means “same line.” …
Choice F
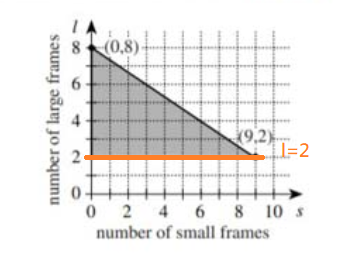
Choice C
$$"Every\ hour"=$3$$ $$ Large=3hrs\times4L=12$$ $$ …
Choice J
The maximum profit is when …
Choice E
$$ab-cb$$ $$x\cdot x-8x=-16$$ $$x^{2}-8x+16=0$$ $$(x-4)(x-4)or(x-4)^{2}=0$$ …
Choice K
$$A=P(1+0.01i)^{n}$$ $$\Rightarrow\frac{A}{(1+0.01i)^{n}}=\frac{P(1+0.01i)^{n}}{(1+0.01i)^{n}}$$ $$\Rightarrow P=\frac{A}{(1+0.01i)^{n}}$$
Choice C
(A) Never true: A positive …
Choice J
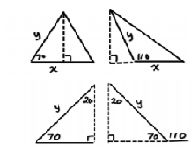
Set x as the base …
Choice E
Here it is the Law …
Choice G
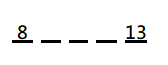
$$\frac{13-8}{4}=\frac{5}{4}$$ $$8=a_{1}+5(\frac{5}{4})$$ $$a_{1}=1.75$$ $$a_{2}=1.75+1.25$$ $$a_{3}=1.75+1.25+1.25$$ …
Choice C
$$(x+3)^{2}=0$$ $$\Rightarrow x^{2}+6x+9=0$$ $$\Rightarrow m=6$$
Choice F
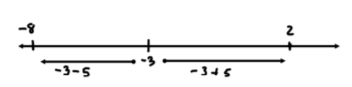
$$\mid x-(-3)\mid=5$$ $$(x+3)=-5 $$ $$(x+3)=5$$ …