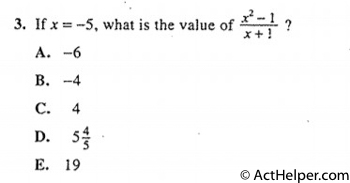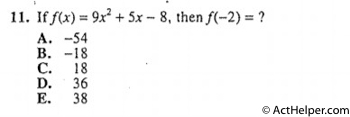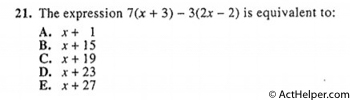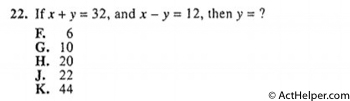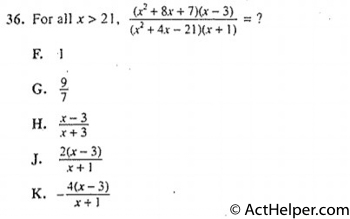Choice A
$$\frac{x^{2}-1}{x+1}$$ $$=\frac{(-5)^{2}-1}{(-5)+1}$$ $$=\frac{24}{-4}$$ $$=-6$$
Choice H
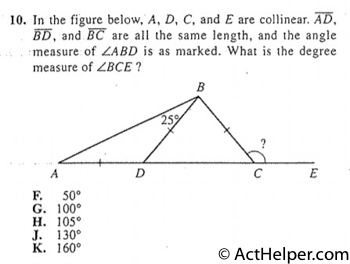
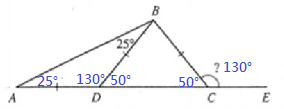
$$(15+6)\times2=42$$
Choice E
$$12(x-11)=-15$$ $$\Rightarrow 12x-132=-15$$ $$\Rightarrow 12x=117$$ $$\Rightarrow 4x=39$$ $$\Rightarrow x=\frac{39}{4}$$
Choice J
$$30=3\times10$$ $$20=2\times10$$ $$70=7\times10$$ $$[30,20,70]=2\times3\times7\times10=420$$
Choice E
$$Originally\ wanted=\frac{x}{2}$$ $$(x\times2)\div\frac{x}{2}=4$$ $$\Rightarrow (x\times2)\div4=\frac{x}{2}$$
Choice E
$$\angle B=90°$$ $$\angle A+\angle B+\angle C=180°$$ $$\Rightarrow \angle A+\angle C=90°$$ $$\because \angle A\gt 43°$$ $$90-43=47$$ $$\therefore \angle C \lt 47°$$
Choice G
$$I. $$ $$(2+1)^{4}+(6+3)^{2}\neq10$$ $$II. $$ $$(2-1)^{4}+(6-3)^{2}$$ $$=(1)^{4}+(3)^{2}$$ $$=1+9$$ $$=10$$ $$III.$$ $$(2\div1)^{4}+(6\div3)^{2}$$ $$=(1)^{4}+(2)^{2}$$ $$=1+4$$ $$=5$$ $$\neq 10$$
Choice A
Assuming that x years have passed...
$$\Rightarrow 20,000+800x=15,200+2,000x$$Choice E
$$=7x+21-6x+6$$ $$=x+27$$
Choice G
$$x+y=32---(1)$$ $$x-y=12---(2)$$ $$(1)+(2)$$ $$\Rightarrow 2x=44$$ …
Choice C
$$(2x-3)^{2}$$ $$=4x^{2}-12x+9$$ $$\Rightarrow a=4,b=-12,c=9$$ $$a+b+c=4-12+9=1$$
Choice H
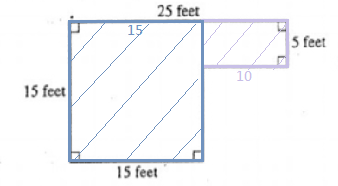
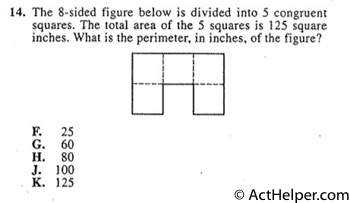
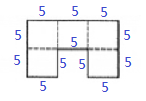
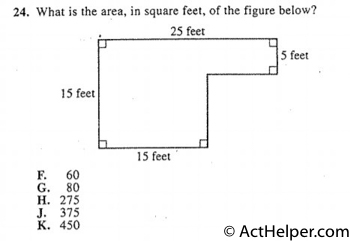
$$\Rightarrow 15\times15+5\times10$$ $$=225+50$$ $$=275$$
Choice A
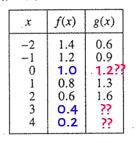
It can be seen from the table that f(x) moves in increments of 0.2, meaning f(x) is a linear function. It follows that f(4) = 0.2.
Choice H
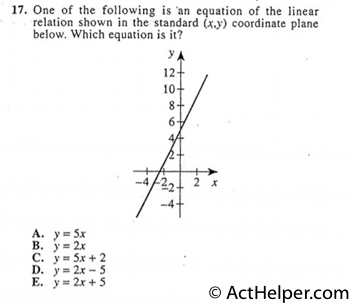
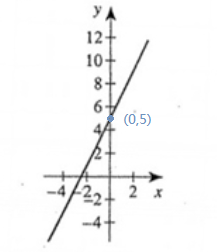
$$y=mx+b$$ $$6y=14x+5$$ $$y=\frac{14}{6}+\frac{5}{6}$$ $$m=\frac{14}{6}=\frac{7}{3}$$
Choice C
$$x^{2}+x-12$$ $$=(x-3)(x+4)$$ $$\Rightarrow x=3,-4$$ $$3+(-4)=-1$$
Choice J
$$3+5+7=15$$ $$\Rightarrow 15\times\frac{5}{3}=25$$
Choice A
$$\Rightarrow -6,-5,-3,-2,1,2,4$$ $$The\ median:\ -2$$
Choice G
$$x^{2}-23(x)=50$$ $$\Rightarrow x^{2}-23(x)-50=0$$ $$\Rightarrow (x-25)(x+2)=0$$ …
Choice B
$$d=\frac{1}{2}at^{2}$$ $$80=\frac{1}{2}(20)t^{2}$$ $$80=10t^{2}$$ $$8=t^{2}$$ $$t\approx2.82$$
Choice F
$$\frac{abc^{2}d}{bcd}=ac$$ $$\frac{a^{2}bc^{3}d}{abc^{2}d}=ac$$ $$\Rightarrow a^{2}bc^{3}d(ac)=a^{3}bc^{4}d$$
Choice D
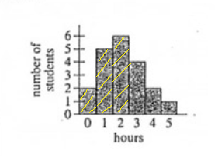
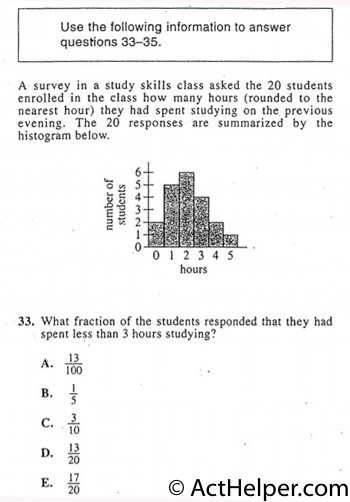
$$\Rightarrow \frac{2+5+6}{20}$$ $$=\frac{13}{20}$$
Choice J
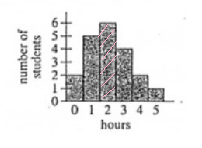
$$\Rightarrow \frac{4}{20}=\frac{2}{10}$$ $$\frac{2}{10}\times360°=72°$$
Choice B
$$=\frac{0(2)+1(5)+2(6)+3(4)+4(2)+5(1)}{20}$$ $$=\frac{0+5+12+12+8+5}{20}$$ $$=\frac{42}{20}$$ $$=2.1$$
Choice F
$$\Rightarrow\frac{(x+7)(x+1)}{(x+7)(x-3)}\times\frac{x-3}{x+1}$$ $$\Rightarrow 1$$
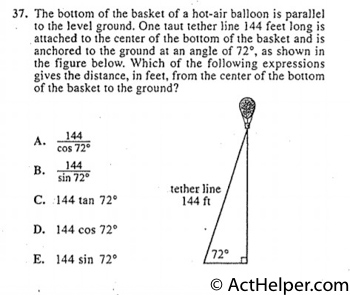
Choice E
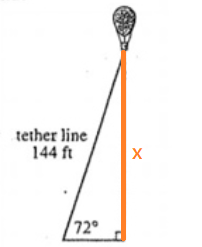
$$\sin 72°=\frac{x}{144}$$ $$x=144\sin 72°$$
Choice G
$$\Rightarrow(\frac{-8+2}{2},\frac{-3+3}{2})$$ $$=(\frac{-6}{2},\frac{0}{2})$$ $$=(-3,0)$$ $$\Rightarrow x=-3$$
Choice B
$$\Rightarrow\sqrt{(-6-(-2))^{2}+(-7-(-3))^{2}}$$ $$=\sqrt{16+16}$$ $$=\sqrt{32}$$ $$\approx 5.65$$ …
Choice K
"The sum of two rational …
Choice B
$$i=\sqrt{-1}$$ $$i^{2}=-1$$ $$\Rightarrow (i^{2})^{2}=1$$ $$\Rightarrow …
Choice H
$$x=3$$ $$y=(3-3)^{2}+2=2$$
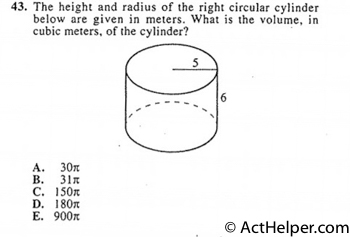
Choice C
$$\pi r^{2}=25\pi$$ $$25\pi\times6=150$$
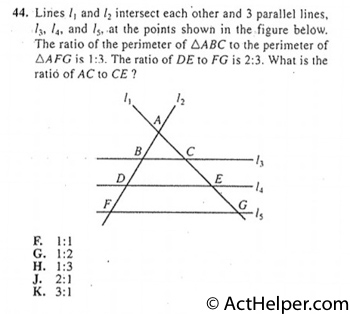
Choice F
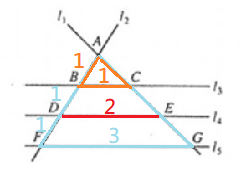
$$The\ perimeter\ of\ \triangle ABC:\triangle …
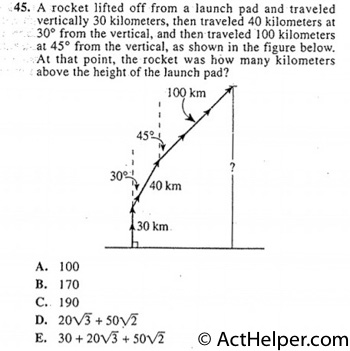
Choice E
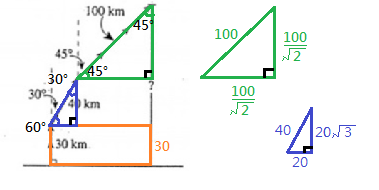
$$\triangle 45°-45°-90°=1:1:\sqrt{2}$$ $$\triangle 30°-60°-90°=1:\sqrt{3}:2$$ $$H=\frac{100}{\sqrt{2}}+20\sqrt{3}+30$$ …
Choice H
The equation of a circle …
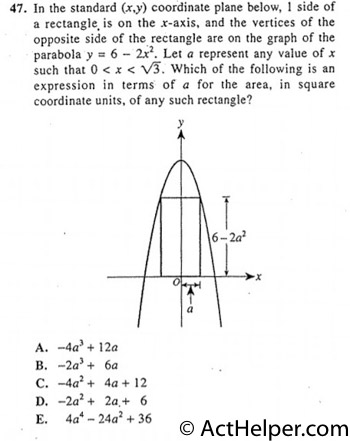
Choice A
$$2a\times(6-2a^{2})$$ $$=12a-4a^{3}$$
Choice F
$$Let n be 2 or …
Choice D
Logarithm base 5 of 5 …
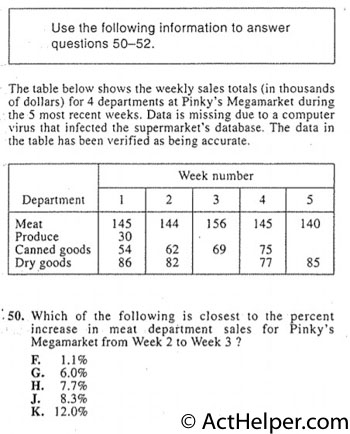
Choice J
$$\frac{156-144}{144}=\frac{12}{144}\approx0.083$$
Choice D
$$\frac{156+145+140+x}{4}=150$$ $$441+x=600$$ $$x=159$$
Choice G
$$Week\ 1=30$$ $$Week\ 2=30(1.1)=33$$ $$Week\ …
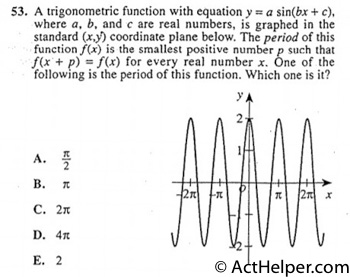
Choice B
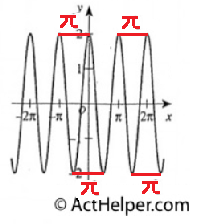
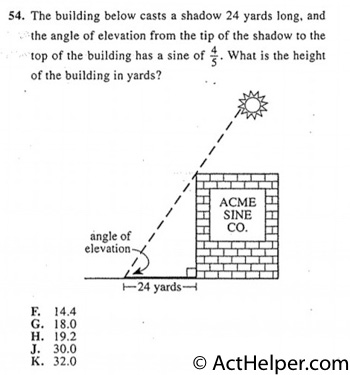
Choice K
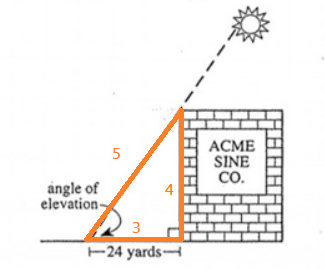
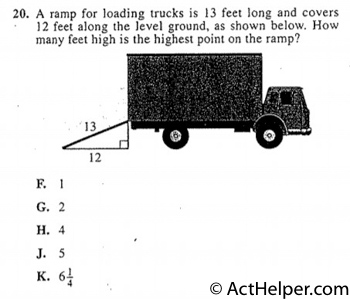
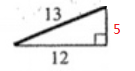
$$3:4:5$$ $$=24:32:40$$ $$The\ height=32$$
Choice C
$$\mid x^{2}-12 \mid -4=0$$ $$\Rightarrow\ …
Choice K
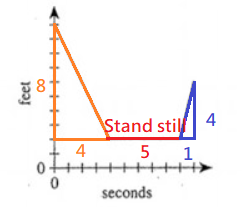
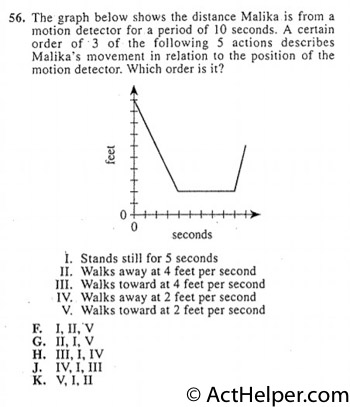
$$10\rightarrow2=Walk\ toward$$ $$Speed=\frac{8}{4}=2$$ $$2\rightarrow6=Walk\ away$$ …
Choice D
$$2:10\rightarrow 5:30$$ $$=3\ hours\ 20mins=3\frac{1}{3}\ …
Choice K
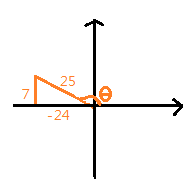
$$24^{2}+7^{2}=25^{2}$$ $$\Rightarrow \sin \phi=\frac{7}{25}$$
Choice B
$$w+z=5$$ $$(w,z)=(1,4),(2,3),(3,2),(4,1)$$ $$2^{w}=x$$ $$x^{z}=64$$ $$(1,4)\Rightarrow2^{1}=2,\ …
Choice F
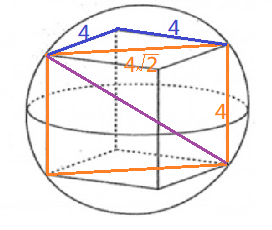
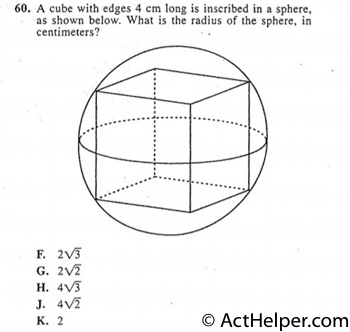
$$\sqrt{(4\sqrt{2})^{2}+4^{2}}=\sqrt{48}=4\sqrt{3}$$ $$4\sqrt{3}=2r$$ $$r=2\sqrt{3}$$